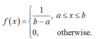Probability

Question 1

______________ can be used to quantify uncertainty.

Answer 1

Probability.

Question 2

The probability of occurrence of a particular event, taken from a finite set of possible events, is _____ if that event is impossible, is ___ if that event is certain, and takes a value somewhere between ____ and ___ if that is possible but not certain.

Answer 2

0, 1: 0, 1.

Question 3

We require that the sum of the probabilities of every possible outcome adds up to ___.

Answer 3

one.

Σ P_i = 1.

Question 4

The expected value (mean) of a discrete probability distribution is …

Assuming all the weights add to 1.

Answer 4

x = Σx_iP_i. The bolding is to represent brackets indicating the average.

Question 5

Assuming that the weights add to 1.

Any function of x can be averaged, using ….

Answer 5

f(x) = Σ f(x_i)•P_i. Where the bold is to represent the brackets indicating the average.

Question 6

Considering continuous probability distributions, what is the requirement of all possible values for it to be normalized?

Hint: For discrete probability distributions, Σ P(x) = 1.

Answer 6

∫ P(x) dx = 1.

Question 7

The mean of any function of x, f(x), can be defined as what for continuous probability distributions?

Assuming that the area under the curve of P(x) dx equal 1.

Answer 7

f(x) = ∫ f(x)•P(x) dx. Where the bolding of f(x) represents brackets indicating the average, mean, expected value.

Question 8

To quantify the spread of values in a distribution is to consider the ____________ from the mean for a particular value of x. This is defined by

x - x, where x is the mean of x.

Answer 8

deviation.

Question 9

The mean squared deviaiton is another name for what?

Hint: <(x - x)²>

Let the mean of x = x.

Answer 9

The variance, σ_x².

<(x - x)²> = ∫ (x - x)² P(x) dx, for a continuous probability distribution and lettingthe mean of x = x.

Question 10

The ________ _________ represents the “root mean square” (known as rms) scatter or spread of the data.

Answer 10

standard deviation.

σ_x = [<(x - x)²>]^½ = x² - (x)², for a continuous probability distribution and letting the mean of x = x.

Question 11

A probability distribution, which is very important in thermal physics is based on what is called a _________ ______, an “experiment” with two possible outcomes.

Answer 11

Bernoulli trial.

Question 12

The ________ ____________ is the discrete probability distribution P(n,k) of getting k successes from n independent Bernoulli trails.

Answer 12

binomial distribution.

Question 13

The ________ ________ of elementary algebra states that (x + y)ⁿ = Σ ⁿC_kx^ky^n-k.

Answer 13

binomial theorem.

Question 14

Binomial Distribution Characteristics, give the mean and standard deviation.

Answer 14

k = np.

σ_k = [np(1-p)]^½

Question 15

The ______________________ is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others.

Answer 15

weighted arithmetic mean

Question 16

Give the weighted mean formula for a discrete random variable x.

Answer 16

x = Σ P_ix_i / Σ P_i

The weights (P_i) with a high weight contribute more to the weighted mean than do elements with a low weight. The weights cannot be negative. Some may be zero, but not all.

Question 17

Give the formula of the weighted average for a continuous random variable x.

Answer 17

x = ∫ P_i(x) x_i dx / ∫ P_i(x) dx

Question 18

A special case of the weighted mean, this case requires that P(x) = 1 and gives the average height of a function. Name the function and give the formula.

Answer 18

Mean value of a function.

f(x) = ^b∫_a f(x) dx / (b - a), where the integral is taken from b to a.

Question 19

What are properties of uniform probability distribution?

Answer 19

1. It is a continuous distribution
2. The probability distribution function is a constant for all values of the random variable x.

(This means that all the events are equally likelyy to occur.)

3. The total area underneath the probability distribution curve is equal to 1.

Question 20

Give an expression for a uniform probability distribution f(x), observing the curve where it has a value only on the range of a <= x <= b.

Answer 20