Homework Problems

Question 1

A magnetic system has specific heat which is a function of applied magnetic field, H and temperature, T.

It can be represented theoretically by

C(T,H) = C(H/T) = N*(H/T)² / cosh²(H/T) where N is constant.

(a) Expand C(T,H) in power of (H/T) up to (H/T)⁴ assuming H << T.
(b) Sketch (freehand) the behavior of your answer as a function of x = H/T.

Answer 1

Question 2

A system contains n atoms, each of which can only have zero or one quanta of energy. How many ways can arrange r quanta of energy when n = 2x10²³; r = 10 ²³?

(How can you arrange the amount of quanta of energy r to the amount of atoms n.)

Answer 2

Question 3

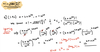
The probability P(n) that an event characterized by a probability p occurs n times in N trials is given by the binomial distribution

P(n) = [N! / n!(N-n)!] pⁿ (1 - p)^N-n.

Consider a case where p << 1 and N >> 1.

(a) Show that (1 - p)^N-n ≈ e^-Np using ln(1-p) ≈ -p.
(b) Show that N!/(N-n)! ≈ Nⁿ .
(c) Therefore, you can show that P(n) = (λⁿ / n!) e^-λ where λ = Np. You have just demonstrated that the binomial distribution for small p and large N turns into the Poisson distribution!

Answer 3

Question 4

Two bodies, with heat capacities C₁ and C₂ (assumed independent of temperature) and initial temperatures T₁ and T₂ respectively, are placed in thermal contact. Show that their final temperature T_f is given by

T_f = (C₁T₁+C₂T₂)/(C₁+C₂).

If C₁ is much larger than C₂, show that

T_f ≈ T₁+C₂(T₂−T₁)/C₁.

Answer 4

Question 5

(3.3) Blundell & Blundell

Answer 5

Question 6

If θ is a continuous random variable which is uniformly distributed between 0 and π, write down anexpression for P(θ). Hence find the value of the following averages:

(d) θⁿ (for the case n ≥ 0)
(g) |cosθ|

Answer 6

Question 7

Find the average energy E for

(a) An n-state system, in which a given state can have energy 0, 2ε, 3ε, …., nε.
(b) A harmonic osillator, in which a given state can have energy 0, 2ε, 3ε, …., (i.e., with no upper limit).

Answer 7

The key to this question is the recongization of the partition function being a geometric series.

Question 8

Find the mass of a hydrogen molecule, given that the atomic weight of one hydrogen atom is 1.01 amu.

Answer 8

In reality, the hydrogen molecule is diatomic.

1.01 amu = 1.01 grams/mole = .001 kg/mole

so

(.001 kg/mole) / N_A ≈ 3.3 x 10^-27 kg.

Question 9

Derive an explaination of the difference between a vertical spring and a horizontal spring.

Answer 9

Use energy conservation to show that you can treat a vertical spring as a horizontal spring. Hooke’s Law can be applied at the equilibrium position when mg = kx_o and we do not need to consider the natural length of the spring to be our starting point as in the horizontal case.

Question 10

Answer 10

A. x = mg/k

B. Classical view for a non equilibrium position: ½k(x-x_o)²

Translational time invariance states PE = KE, since the only force is conservative.

So in terms of statistics then we take the average of x and the equilibrium point x_o labled as (x-x_o) which is named as a fluctuation/deviation.

½k(x-x_o)² = ½K_BT = E_particles

⇒ (x-x_o) = (K_BT/k)^½.

C. m = (K_BkT)^½/g

Question 11

Answer 11

Question 12

A) What is the volume occupied by 1 mole of gas at 10^-10 torr, the pressure inside an “ultra high vacuum” (UHV) chamber?

B) Calculate the average distance between the molecules.

Answer 12

Assuming T ≈ 300K,

V ≈ 1.875 x 10¹¹ m³ (a macroscopic quanity)

n = 1/V (Proportions and ratios)

r ≈ 4.20 x 10^-5 m.

Question 13

A diffuse cloud of neutral hydrogen atoms (known as HI) in space has a temperature of 50K and number density 500 cm^-3. Calculate the pressure (in Pa) and the volume (in cubic light yrs) occupied by the cloud if its mass is 100M_sun.

M_sun ≈ 1.99 x 10³⁰ kg

1 light yr. ≈ 9.460 x 10¹⁵ m

Answer 13

Question 14

Answer 14

For B) you know the average energy to be 3 · ½k_BT, Ch. 5. To find the average energy of those hitting the wall, use the proper integral dervived in Ch. 6.