Principles of Diffraction

Question 1

Describe diffraction.

Answer 1

Diffraction is the process by which a system of waves is spread out by interaction with matter.

If we can create a lens, e.g. in a microscope, then the diffracted waves can be used to recreate an image. Otherwise, we can only measure the waves and reconstruct using a computer e.g. with x-rays and other forms of radiation.

Question 2

What is the 2-slit (2-atom) experiment?

Answer 2

• when there’s one origin of diffraction, we get one source of waves spreading out from the origin in all directions
• when there’s light shining through a second slit/onto a second atom, we get another source of waves spreading out from the second origin
• when we have radiation spreading out from both sources at once we get interference between the waves
  
  • in some directions the waves add (constructive) to give strong peaks and troughs
  • in some directions the wave cancel (destructive)
• different sources give different patterns

Question 3

Why use crystals?

Answer 3

Problem:

• any interaction with an atom, which can tell us about where that atom is, will also damage the atom

Solution:

• observe lots of copies of the molecule in the same orientation at once = a crystal

Question 4

Describe waves.

Answer 4

Waves are defined by three properties:

• wavelength
• amplitude
• phase

Two of these correspond to properties of radiation when considered as particles:

• wavelength - related to photon energy (high E = short wavelength)
• amplitude - proportional to number of photons

Question 5

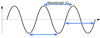
Describe wavelength.

Answer 5

The distance over which a wave’s shape repeats - also the distance between successive peaks or troughs.

For diffraction experiments, we work with monochromatic radiation so we can treat this as constant.

Question 6

Describe amplitude.

Answer 6

The amplitude of a wave describes how high the peaks and troughs are. It relates to the strength of the electromagnetic radiation, i.e. the number of photons. It is always positive.

Question 7

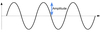
Describe phase.

Answer 7

The phase of a wave describes where the peaks and troughs are located (relative to some arbitrary reference position).

Phase is cyclic - if the wave is shifted by one complete wavelength then you get back to where you started. Therefore, phase is expressed as an angle - 360^o gets you back to where you started.

Question 8

How can waves be described mathematically?

Answer 8

For a given wavelength, a wave can be represented by two numbers: a positive amplitude and a cyclic phase.

The wave can therefore be written in terms of a trigonometric function using amplitude (A) and phase (φ).

Question 9

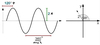
Other than a trigonometric function, how else can a wave be described?

Answer 9

Amplitude and phase (angle) can also describe a vector in a plane using polar coordinates. Therefore, we can describe a wave by polar coordinates (A,φ) or in the complex plane by real and imaginary parts (Argand diagram).

Question 10

Describe why understanding diffraction is important and what it entails.

Answer 10

To see atoms, we need to use short-wavelength radiation (or particles) but we don’t have a lens. Therefore, we need to understand the physics of diffraction to infer what arrangement of atoms would lead to a specific diffraction pattern.

Diffraction from two point scatterers:

• the incident beam is assumed to be coherent i.e. the waves are all in phase
• in the scattered beam, the wave may or may not be in phase
  
  • if all are in phase = strong scattering in that direction
  • if all are out of phase = no scattering in that direction

Question 11

Describe the interference of waves aka what happens when multiple waves combine?

Answer 11

1. if the phases match, we get reinforcement (constructive interference)
2. if the phases differ by 180^o then we get cancellation (destructive interference)
3. if the phases differ by some other amount then we get a wave that is weaker than the amplitude sum and is of intermediate phase - the combined wave can always be determined by adding the vectors

Question 12

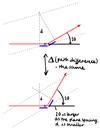
Describe path difference and its effect on interference.

Answer 12

• Path difference = difference in distance travelled by the two waves from their respective sources to a given point on the pattern.
• When the path difference (d) is a whole number of wavelengths (Δ= nλ) we get constructive interference
• When the path difference is a half number of wavelengths (Δ = (n+1/2)λ) we get destructive interference

Question 13

What is Bragg’s law?

Answer 13

Consider diffraction from crystal planes, rather than emission from 2 slits.

The diffracted (scattered) beams are in phase (i.e. strong diffraction) when the path difference is a whole number of wavelengths, i.e.

nλ = 2d sin(θ)

This is Bragg’s law.

Question 14

What are the key points about Bragg’s law?

Answer 14

1. Despite how they’re usually drawn, the atoms don’t need to line up; the path difference is the same wherever the atoms are on the planes. The only thing that matters is the distance between planes of similar atoms
2. Scattering from subsequent layers of planes leads to increasing path differences represented by n > 1 in Bragg’s equation.
   
   • if scattering from the first plane is in phase (n = whole number) then scattering from every subsequent plane will also be in phase

Question 15

Describe a diffraction experiment.

Answer 15

• rotate the picture by θ to reflect the experiment
• the incident x-ray beam is fixed, but we can measure diffraction spots appearing in different directions around the crystal
• the angle of diffraction is 2θ

Question 16

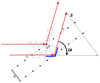
What is ‘s’?

Answer 16

• diffraction vector = difference between incident and reflected beams
• describes the position of the diffraction spot
• always perpendicular to the corresponding crystal plans
• the length of s is inversely proportional to plane spacing, d

Question 17

Describe the angle of diffraction.

Answer 17

Angle of diffraction, 2θ, gets larger as the plane spacing, d, gets smaller.

I.e. the highest angle diffraction spots correspond to the closest together planes.

Question 18

What are the components of an x-ray diffraction experiment?

Answer 18

• x-ray source
• filter/monochromator
• collimator
• sample/goniometer
• beamstop
• detector

Question 19

What are the two ways of generating an x-ray source?

Answer 19

• bremsstrahlung/breaking radiation
• Siegbahn notation

Question 20

Describe creating an x-ray source via bremmsstrahlung/breaking radiation.

Answer 20

• electromagnetic radiation is produced when a charge is accelerated
• x-rays can be produced by accelerating electrons from a cathode to an anode using a high voltage
  
  • the deceleration of the electrons on hitting the anode gives off x-rays
  • for higher intensities a rotating anode is used to limit heating of the anode by the electron beam

Question 21

Describe creating an x-ray source via Siegbahn notation.

Answer 21

• characteristic radiation is produced when an outer shell electron fills a vacancy in an inner shell
• Cu and Mb are most used for lab sources

Question 22

How can higher intensity x-rays be produced?

Answer 22

• synchrotrons provide much higher intensity (often tunable) x-ray sources for macromolecular crystallography
  
  • originally from bending magnets which accelerate the electrons in a circle
  • now, insertion devices such as undulators are used for even more intense radiation

Question 23

Describe a filter/monochromator in an x-ray diffraction experiment.

Answer 23

• at a synchotron, a two-crystal monochromator uses Bragg diffraction to select different wavelengths by changing the angle of diffraction.
  
  • e.g. a nickel filter will allow the Cu K-alpha radiation through while blocking the K-beta

Question 24

How can you scan the diffraction pattern in an x-ray diffraction experiment?

Answer 24

• a four circle diffractometer has 4 angles which can be changed to excite different diffraction spots
• a mini-kappa goniometer is a simple version of the same concept
• originally, these were used with ‘point’ detectors, but area detectors allow us to produce 2D slices of the diffraction pattern
• a 3D crystal gives rise to a 3D diffraction patter, so with a 2D detector we technically only need to vary one more angle

Question 25

Describe a beamstop in an x-ray diffraction experiment.

Answer 25

• the beamstop prevents the x-ray beam from damaging (or burning a hole in) the detector.

Question 26

Describe the different x-ray detectors in an x-ray diffraction experiment.

Answer 26

• point detectors
• line detectors e.g. CCD
• area detectors e.g. CCD
  
  • CCDs need protecting from x-rays
• detectors need to be much larger than typical camera sensors
• photon counting (area) detectors are most sensitive

Question 27

What makes up a crystal?

Answer 27

Crystal = Lattice + Motif

The crystal lattice is the pattern of repeated features which assemble to form the crystal.

The crystal also arises from a ‘motif’ which is repeated at each position in the 3D (2D) lattice, to create the whole crystal.

Question 28

How can we describe the structure of a crystal?

Answer 28

• in order to describe the structure, we need to describe the lattice and the motif
• the lattice consists of repeats of the motif so we break it down into a ‘unit cell’ or building block which can be tiled in 3D to reconstruct the entire crystal
• the unit cell is an imaginary concept - we can choose to base it on any point in the crystal

Question 29

Describe the conventions of a crystal lattice.

Answer 29

A lattice is defined by vectors a, b and c, which are the edges of the unit cell in 3D. Conventions:

• the unit cell must be a complete ‘building block’
• the crystal must be reproducible by applying combinations of the a, b and c vectors to the unit cell
• the axes a, b and c must be right handed
• best compromise between:
  
  • the unit cell should have the smallest possible volume
  • the unit cell should have the highest possible symmetry

Question 30

Describe the vectors a, b, and c and their angles

Answer 30

• a, b and c are vectors in angstroms
• α is the angle between b and c
• β is the angle between a and c
• γ is the angle between a and b
• angles are reported in degrees

Question 31

Describe the different coordinate systems.

Answer 31

Orthogonal coordinates:

• measured in angstroms
• along x, y, z directions
• easy to calculate distances using Pythagoras

Fractional coordinates:

• measured as fraction of the cell edge
• along a, b, c directions
• easy to shift coordinates to another cell or apply symmetry

Convert using ‘orthogonalisation matrix’ or its inverse.

Question 32

How can crystal planes be described?

Answer 32

• the repeating crystal lattice means that certain planes cutting through the crystal will also show repeating features - crystals will tend to cleave along these planes to give smooth faces
• Such planes can be described by a unit cell (shape) and a set of 3 integers (hkl), each integer is the number of times the plane cuts the corresponding cell axis
• negative numbers often written as e.g. 1^- to indicate that the axis needs to be reversed
• higher integers N indicate that the axis is cut at 1/N, so the planes cut the axis N times

Question 33

How does the diffraction vector s change for different sets of Miller planes and what does this change?

Answer 33

• length of s is inversely proportional to plane spacing, d, so closer planes gives larger s
• s tells us where the diffraction spot will be
• s is perpendicular to the corresponding planes
• e.g. (100) vs (200)
  
  • (100) - s is perpendicular to the (100) planes and the length is the reciprocal of the distance between the planes, so the diffraction spot will represent this
  • (200) - d is half the size so s is double in length compard to (100), the diffraction spot will be in the same direction from the origin but twice the distance away

Question 34

What is a consequence of the diffraction vector s changing with different sets of Miller planes?

Answer 34

• the diffraction pattern formed from the different diffraction spots forms a 3D latice with orthogonal directions and reciprocal spacings to the crystal lattice
• this is called the reciprocal lattice, with vectors a*, b*, c*
  
  • a* perpendicular to b and c
  • b* perpendicular to a and c
  • c* perpendicular to a and b

Question 35

Describe the resolution of a diffraction spot and therefore the whole pattern.

Answer 35

• the ‘resolution’, d_min, of an individual diffraction spot is the separation of the closest pair of Bragg planes producing that reflection
  
  • it is related to the angle of diffraction, 2θ, for that reflection through the Bragg equation
• the resolution of the diffraction pattern is the resolution of the highest resolution ‘largely’ complete sphere of reflections
  
  • number of reflections increases as an inverse cube of resolution

Question 36

What is the Ewald sphere and why does it occur?

Answer 36

• we observe a curved pattern (‘lunes’) of spots even though the diffraction pattern lies on a regular grid
• for any single orientation of the crystal in the beam, the diffraction vectors that can be stimulated lie on the surface of a sphere
• the observed diffraction pattern for any orientation is therefore a spherical slice through the 3D reciprocal lattice
• curved slice = Ewald sphere
• lunes arise when groups of reflections cross this sphere

Question 37

How does a diffraction pattern tell us about the crystal lattice and the motif?

Answer 37

• we have already seen that the arrangment of the spots (‘reflections’) tell us about the crystal lattice
• the different spots have different intensities which is due to the motif
  
  • to understand this, we need to be able to quantify the interference between waves

Question 38

How can we do sums with waves?

Answer 38

• we convert each wave to x-y components in the Argand diagram using Euler’s formula, then add up the x and y components
• convert back to an amplitude and phase

Question 39

Determine the sum of the following two waves:

1. Amplitude 5, phase 30^o
2. Amplitude, 5, phase 120^o

Answer 39

Question 40

What is the method for calculating the diffraction pattern from an arrangement of atoms?

Answer 40

• start by picking an arbitrary origin in the crystal e.g. corner of unit cell
• work out the phase of a ray diffracted in a given direction from a given point in the unit cell, relative to the phase of a hypothetical ray diffracted from the origin
  
  • assuming point atoms, sum the diffracted waves from each atom in the unit cell, taking into account their phase to determine constructive/destructive interference
  • or, integrate the diffracted waves from every point in the unit cell, based on the electron density at the point in the cell

Question 41

Derive the equation for the path difference in terms of the incident and diffracted beams.

Answer 41

Question 42

Using the equation for the path difference, derive an equation for the phase difference in terms of the diffraction vector, s.

Answer 42

Question 43

Once the equation for the phase difference is in terms of s, what other trick can be used?

Answer 43

Question 44

Describe the structure factor equation.

Answer 44

Question 45

What is the problem with the structure factor equation?

Answer 45

It assumes point atoms. In reality, atoms have a finite size as their electron density is spread out. Spreading out is equivalent to limiting the resolution of the diffraction pattern in the reciprocal space. We can therefore include the effect of atomic shape by making f_j decrease with resolution, i.e. with distance of diffraction spot h from the origin of the pattern.

Question 46

Describe form factors.

Answer 46

For reflections closest to the origin, the form factor is proportional to the number of electrons.

As resolution increases (i.e. reflections further from the origin), the form factor drops off quickly for large atoms or slowly for small atoms.

Reciprocal relationship:

• small atom = large scattering radius
• large atpm = small scattering radius

Question 47

What happens if we don’t want to assume spherically symmetric atoms?

Answer 47

We have to start from a 3D ‘map’ of the electron density in the unit cell, or ‘electron density map’, and the sum scattering from every point in the cell by integration. We call the electron density map ρ(x), where x is the fractional coordinate.

Question 48

Describe a fourier transform in terms of ρ(x).

Answer 48

Question 49

Describe the Fourier transform describe?

Answer 49

Tells us how some signal can be decomposed into frequency components i.e. into waves of different frequencies, amplitudes and phases.

It describes an abitrary 1D or 3D graph in terms of waves, whose peaks lie on the Bragg planes.

We can make any repeating function from the right combo of sine wives. The amplitude and phase of the required waves are given by the amplitude and phase of the corresponding spots in the diffraction pattern.

Question 50

What does the diffraction pattern show?

Answer 50

• how ‘wavey’ the electron density is in a particular direction with a particular spacing
• the amplitudes tell us about the spacing of the features in the unit cell
• the phases tell us about where the features are in the unit cell

Question 51

Describe data collection/processing in structure solution by x-ray crystallography.

Answer 51

• collect images with different orientations to get different slices through the 3D diffraction pattern
• from the spot spacing, infer the unit cell dimensions
• predict the expected positions of spots in every image
• integrate the intensity of each spot by summing pixels at the predicted position

Question 52

What the data quality measures in data collection/processing?

Answer 52

• completeness - the proportion of reflections at a give resolution which were actually measured
• R_sym + R_merge - agreement between different observations of the same spot
• standard deviation of each observation is the standard error estimate for I(h)
• resolution - the radius where the spots contain more noise than signal

Question 53

Describe mosaicity.

Answer 53

Crystals are not monolithic, but composed of mosaic blocks. These cause a spread in the orientation of the Bragg planes, and therefore spreading of the diffraction spots. Sometimes this can cause spots to overlap.

Mosaicity is estimated as part of the data collection.

Question 54

What is the phase problem?

Answer 54

To calculate an electron density map, we need both the amplitude, |F(h)|, and the phase, φ(h), because

F(h) = |F(h)| exp(i φ(h))

We can observe the intensity, I(h) = |F(h)|², but we don’t know the phase, φ(h).

Question 55

Describe the Patterson method for solving the phase problem.

Answer 55

If we calculate an electron density map using |F(h)|² (i.e. intensities) instead of |F(h)| (amplitudes), and settling the unknown phase to zero, then we are keeping the spacing info but losing the positional info.

The result is a ‘vector map’ of the structure - a map of interatomic distances. For simple structures, we can often decode this to get the structure. The number of peaks is proportional to the square of the number of atoms, limiting applicability to larger structures.

Question 56

Describe direct methods for solving the phase problem.

Answer 56

Question 57

Describe the heavy atom method for solving the phase problem.

Answer 57

If the structure includes a small number of much heavier atoms, they will dominate the scattering.

• solve for heavy atoms by Patterson or direct methods
• use to get initial phases
• find the rest of the structure by refinement/rebuilding

Only useful for small molecules.

Question 58

Descibe molecular replacement for solving the phase problem.

Answer 58

Used for macromolecules.

• find a similar (known) structure on the basis of evolutionary relationships/protein sequence similarity
• place it in the unit cell to reproduce the observed diffraction pattern as closely as possible
• fix the remaining differences by looking at difference maps and by refinement/rebuilding

Question 59

Describe using substructure (experimental) phasing for solving the phase problem.

Answer 59

Used when there’s no solved molecule similar to the molecule of interest.

• find the arrangement of a small number of special scatters
  
  • heavy atoms
  • anomalous scattering
• infer (weak) phase info
• calculate a (noisy) map

Question 60

Describe refinement/rebuilding in structure solution by x-ray crystallography.

Answer 60

If we have approx. phases we can use them along with observed structure factor amplitudes to calculate an electron density map.

This will show where the model needs correcting.

Difference maps are also used to identify where there are errors in the model.

Question 61

Describe refinement.

Answer 61

Question 62

Describe the R-factor for different sized molecules and how it can be improved when resolution is poor.

Answer 62

• small molecules - R < 10 %, some < 3 %
• macromolecules - R < 10x the resolution as a percentage

When resolution is poor, we can improve the R-factor by adding more parameters to the model because we can refine these to improve the fit.

e.g. for macromolecules - split into ‘work’ and ‘free’ sets, calculate R-factors for both sets, if we are using too detailed a model for the number of observations then R_free >> R_work (bad).

Question 63

Describe temperature factors.

Answer 63

• B factor: ‘temperature’ factor
• smears out the electron density of an atom to simulate the thermal motion of that atom
  
  • can be isotropic or anisotropic
• B = 8 π² < r - r₀ >²
  
  • < r - r₀ >² = mean square replacement in Ų
• causes a faster drop off in the scattering factor, f

Question 64

Describe the observation/parameter ratio.

Answer 64

General rule: you can never determine more parameters than you have observations.

Errors/uncertainties in the observations lead to errors in the parameters; excess observations lead to reduced uncertainties.

Question 65

Describe validation.

Answer 65

Question 66

Describe stereochemical restraints.

Answer 66

When obs/par ratio < 10, we use stereochemical restraints to increase the number of observations or decrease the number of parameters.

We also restrain neighbouring B factors.