Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Core 9 > Inorganic Materials and Nanoparticles > Flashcards

Inorganic Materials and Nanoparticles Flashcards

1
Q

Describe crystallinity.

A

Solids exhibit a continuum of order from perfect crystals to totally amorphous.

  • long range order = crystalline (e.g. SiO2 as quartz)
  • short range order = amorphous (e.g. SiO2 as glass)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Describe structure types.

Give an example.

A

Structures of compounds can be divided into classes. Traditionally, each class is named after an archetypal compound or mineral.

e.g. ReO3 is built from vertex sharing ReO6 octahedra. Any other compound that exhibits this type of structure (e.g. NbF3) is called a structure type. NbF3 has ReO3 structure type.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Define polymorphism.

A

Some solid compounds can have more than one crystalline structure for a single stoichiometry, called polymorphism. Individual structures are called polymorphs.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Give an example of polymorphs and some key facts about polymorphs.

A
  • Rutile, anatase and brookite are all polymorphs of TiO2
  • individual polymorphs will be thermodynamically stable at a particular p and T
  • other polymorphs can have kinetic stability at the same p and T
  • often, a solid having a particular crystalline structure and stoichiometry is referred to as a phase
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Give some general points on structure and charge of a bulk solid.

A
  • for ionic solids, the anions are much bigger than the cations so the anions are close packed while the cations fit into the interstitial sites (the cations will be more mobile)
  • in drawings, lines don’t always mean a bond they may describe coordination
  • the overall charge of a bulk solid will be zero, however charge can be distributed heterogeneously
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Describe general defects and non-stroichiometry.

A
  • only at 0 K will an ionic crystal have a perfectly ordered array of atoms where every atomic lattice point contains an atom
  • at > 0 K crystals contain defects
  • defect formation requires energy and is always endothermic
  • however, a structure with defects has higher entropy
  • increased entropy drives defect formation to ΔG = 0
  • strong T dependence on number of defects
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

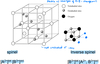
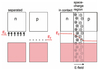
Describe intrinsic point defects.

A
  • vacancy: an ion is missing
  • interstitial: an extra ion is present in the interstitial site
  • Schottky: a pair of vacancies are present in the lattice
  • Frenkel: a defect pair is created by an ion (usually cation) moving into an interstitial site
  • the lattice will distort at the vacancy site to minimise the loss in lattice energy
  • vacancy and interstitial atoms do not have to be adjacent and can be mobile
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

What is the equation for the proportion of defects?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Describe the percentage of intrinsic point defects in ionic compounds.

A
  • in most ionic compounds, the percentage of intrinsic point defects is small but they can have a significant effect on electrical, magnetic and optical properties
  • the smallest ΔH (ΔHS or ΔHF) will determine if Schottky of Frenkel defects dominate
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Describe extrinsic point defects.

Give an example.

A
  • introducing different ions into the structure - known as doping
  • Si (group 14) is not a good electrical conductor
  • if Si is doped with small amounts of P (group 15) then the conductivity increases significantly
    • an occupied state is introduced just below the Si conduction band
    • after forming bonds to Si, the remaining electron from P acts as a conduction electron
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Describe non-stoichiometry.

Give and example.

A

Defects and doping result in non-stoichiometric solids. It is common for compounds of transition metals that can have variable oxidation states.

e.g. TiO - rock salt structure over the range TiOX (0.7 < x < 1.25).

Non-stoichiometric compounds are distinct from other compositions e.g. TiO2 because they have a common structure. However, lattice parameters of the structure will change gradually as the ratio of elements changes.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Describe solid solutions.

A

Commonly observed in non-stoichiometric solids. A solid solution is a crystalline solid that can have continual varibale composition for a given structure type.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Describe the two types of solid solutions.

A

Substitutional:

  • new atom replaces an existing atom e.g. by doping
  • e.g. Al2O3 and Cr2O3 over the range (Al2-xCrx)O3 (0 < x < 2)
  • similar size and charge allows Cr to occupy the same crystallographic sites as Al

Interstitial:

  • an atom is added to an interstitial site
  • e.g. C in Fe giving FeCx (0 < x < 0.09)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

What is dynamics in solids?

A
  • above 0 K, atoms and ions in compounds move and respond to external stimuli (e.g. magnetic/electric fields, pressure, temperature)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Lithium ion batteries are an example of long range movement of ions. What is this?

A

Batteries comprise of two electrodes and an electrolyte. The Li+ ions must be mobile in all the electodes and electrolyte materials.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Describe intercalation/deintercalation.

A
  • species can be added/removed from a host structure
  • needed for charge/discharge cycles
  • important structural features: layers, channels or porosity provide space for Li+ to move
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

What are the equations for Ecell (V), power (W) and charge (Ah)?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

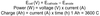
What are the equations for energy (Wh), energy density and specific energy?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What are the challenges in battery science?

A
  1. intercalation/decalation should not result in big structural changes - leads to mechanical stress, fracture and performance loss
  2. avoid uncontrolled Li metal growth (dendrites) = leads to shorting and probable ignition of flammable electrolye
  3. interfaces between electrodes and electrolyte are critical - growth of secondary layer of electrodes helps to prevent degradation of electrolyte (upon contact with strongly reducing and oxidising electrodes) and growth of Li dendrites
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Descibe bulk polarisation.

A

When an ion is in an asymmetric site, there will be a local dipole moment.

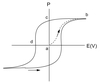
To obtain bulk polarisation (P), the material must have a non-centrosymmetric crystal structure otherwise the local dipoles cancel out. Any process that changes the relative position of ions will change the polarisation.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What are the three different things that dipoles can respond to and what are they called?

A
  • ferroelectrics - dipoles respond to an electric fireld
  • piexoelectrics - dipoles respond to pressure
  • pyroelectrics - dipoles respond to heat
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Describe ferroelectrics.

A
  • can retain polarisation (P) after the electric field has been removed
  • have a very high dielectric permittivity, εr
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Describe the properties of a good dielectric material.

A
  • should have high dielectric strength (not breakdown at high voltages and become electron/ion conducting)
  • have low dielectric loss (not lose electrical energy as heat in an alternating electric field)
  • the stored charge can be measured in a parallel plate capacitor and the dielectric permittivity, εr, measured
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

Give an example of a ferroelectric.

A

BaTiO3 - has the perovskite ABO3 structure.

  • at temperatures above 120oC, the Ti atoms are in a symmetric octahedral site (centrosymmetric)
  • between 5 - 120oC, the Ti atoms are displaced along on of the axes of the octahedron and polarisation results (non-centrosymmetric)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

Why does the structure of a ferroelectric distort?

A
  • the structure of a compound is dependent on the size, charge and preferred coordination number/geometry of the ions
  • for compounds with several elements, the ideal preferences for each ion may not be accommodated and strain may be preent
  • significant strain results in a structural distortion
  • for TM oxides, distortions can be estimated using a tolerance factor
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

Describe the tolerance factor for a perovskite ABO3 structure.

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

How can the polarisation of ferroelectrics be removed?

A

By the application of an opposing electric field. Ferroelectrics exhibit hysteresis which allows charge to be stored.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

What does the graph of a ferroelectric look like?

A
  • a* to b: Apply electric field and individual dipoles are aligned. At b, the sample has reached saturation polarisation.
  • b* to c: Electric field is returned to 0 by the sample remains polarised. This is known as the remanent polarisation.
  • c* to d: In order to depolarise the sample, a field in the opposite direction is required. This is the coercive field.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

Describe piezoelectrics.

A
  • polarise under the action of mechanical stress and develop electrical charges on opposite crystal faces (i.e. voltage difference)
  • when an electric field is place across a piezoelectric crystal, it develops strain
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

What compounds are commonly piezoelectric compounds?

A

Many compounds composed of tetrahedral groups distort under stress and are piexoelectric. Also, tetrahedra don’t have a centre of symmetry and often lead to non-centrosymmetric structures. An example is α-quartz.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Describe pyroelectrics.

A
  • they exhibit a net bulk spontaneous polarisation that is temperature dependent
  • thermal expansion or contraction of the lattice changes the size of the dipoles
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

Give an example of a pyroelectric material.

A

ZnO, with the qurtzite structure.

The ZnO4 tetrahedra (dipoles) point in the same direction, giving rise to a net bulk polarisatio. In contrast to ferroelectrics, the polarisation of pyroelectrics cannot usually be reversed by the action of an electric (coersive) field.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

Describe magnetic behaviour.

A
  • TMs and lanthanides can have partially filled valence orbitals that result in unpaired electrons and magnetism
  • for materials, the collective interaction of ions is key - the strength and direction of the interaction will depend on the spatial relationship (crystal structure) and the mechanism for magnetic exchange
  • the angular momentum (J) of unpaired electrons gives rise to magnetic behaviour
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

Describe the magnetism of individual ions.

A
  • individual ions with unpaired electrons have a magnetic dipole moment (μ)
  • the size of μ depends on the spin and orbital angular moments
  • the orbital angular momentum is due to the motion of the electron about the nucleus
  • in many compounds (esp. first row) the orbital angular momentum is almost entirely quenched because the d-orbitals are no longer degenerate
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

What are the two equations for magnetic dipole moment (μ) for individual ions?

A
36
Q

Describe magnetic susceptibility.

A
  • magnetic susceptibility, χ, is a measure of how magnetic a material is
  • χ varies with temperature (and applied external magnetic field) for different types of magnetism
37
Q

Describe paramagnetism.

A
  • observed for compounds that contain unpaired electrons and where the magnetic dipoles do not interact with each other
  • a paramagnet is attracted to an external magnetic field
38
Q

Describe how paramagnetism changes with temperature.

A
  • as the temperature decreases, the dipoles begin to align parallel (lowest energy configuration) to an external field
  • paramagnetism is temperature dependent
39
Q

Describe antiferromagnetism.

A
  • an example of cooperative magnetism
  • no applied field (H) is necessary to align the dipoles (spins) anti-parallel
40
Q

Describe how antiferromagnetism changes with temperature.

A
  • TN is the Neel temperature (antiferromagnetic-paramagnetic transition temperature0
41
Q

Describe ferromagnetism.

A
  • an example of cooperative magnetism
  • no applied field is necessary to align spins parallel
42
Q

Describe how ferromagnetism changes with termpature.

A
  • TC is the Curie temperature (ferromagnetic-paramagnetic transition temperature)
43
Q

Describe ferrimagnetism.

A
  • an example of cooperative magnetism
  • no applied field is necessary to align spins
  • the alignment is essentially non-parallel, giving partial cancellation of ‘up’ and ‘down’ spins
44
Q

Describe how ferrimagnetism changes with temperature.

A
45
Q

Describe superexchange.

A
  • where anions mediate magnetic exchange between metal cations
  • anions can be sulphur and fluorine, but most commonly oxygen
  • occurs via overlap of atomic orbitals of the oxygen (p-) and metal (d-) atoms
46
Q

Describe how superexchange leads to antiferromagnetism.

e.g. first row TM monooxides that adopt the rock salt structure, where the metal and oxygen are in octahedral sites.

A
  • two eg orbitals containing an unpaired electron overlap with an O2- p-orbital containing two oppositely aligned electrons
  • the spins align themselves to be antiparallel, giving an overall antiferromagnetic exchange coupling
  • below TN, the sublattice structure can be determined experimentally using neutron diffraction
  • above TN, thermal energy > superexchange interaction so the spin no longer align = paramagnetic behaviour
47
Q

Describe the spinel and inverse spinel structure types.

A
  • the structure is based on a cubic close packed arracy of anions
  • the spinels and inverse spinels are then constructed by filling 1/8 of the tetrahedral and 1/2 of the octahedral sits in an ordered manner
  • spinel structural type has the formula AB2X4
48
Q

What factors influence the preference for normal or inverse spinel structures?

A
  1. from electrostatics, M3+ should prefer the octahedral site and M2+ the tetrahedral site
  2. the smaller cation would generally go in the smaller tetrahedral site
  3. crystal field stabilisation energies (CFSEs) - which ion prefers the octahedral site?
49
Q

How can we estimate the magnetic moment of ferrimagnets?

A

Using μ = gS as a rough estimate, we can calculate μ for each ion. The saturation (max) magnetic moment (μsat) for a ferrimagnet is then a vector sum of the individual ion moments. We need to know how the spins couple wrt e/o.

  1. the coupling between octahedral sites is weak, also weak between tetrahedral sites
  2. superexchange between the Oh and Td ions is strong, giving antiferromagnetic alignment
  3. therefore, all Oh ions (A) in the same direction, all Td ions (B) in the same direction but opposite to A
  4. add all octahedral μion, subtract tetrahedral μion
50
Q

What are domains?

A

Below TC, magnet materials are divided into domains. Each domain has ions aligned parallel, but in the absence of an external magnetic field the domains are not parallel to each other. Entropy drives the formation of domains.

On the application of an external magnetic field (H) the domains align in the same direction as the field. When all of the domains are parallel the magnetisation M is at a maximum (saturation magnetisation). M is the magnetic dipole moment per unit volume.

51
Q

What are M vs H curves?

Describe what they show.

A

M vs H are hysteresis curves.

  • a* to b: The domains of a sample are aligned in a magnetic field. At b, the sample has reached saturation magnetisation.
  • b* to c: The field is returned to 0 but the sample remains magnetised. This is called remanent magnetisation.
  • c* to d: In order to demagnetise the sample, a field in the opposite direction is required. This is called the coercive field.
52
Q

Compare hard vs soft magnets.

A
  • Hard magnet: large remanent magnetisation and large coercive field
  • Soft magnet: small remanent magnetisation and small coercive field
53
Q

Describe conductivity (σ) as a function of temperature.

A
  • Insulator: σ < 10-9 Sm-1, conductivity increases with T
  • Semiconductor: σ = 103 - 10-3 Sm-1, conductivity increases with T
  • Metal: σ > 107 Sm-1, conductivity decreases with T
54
Q

Describe band theory.

A
  • overlap of large numbers of atomic orbitals giving ‘band’
  • band orbitals are not distributed evenly in a band - fewer at the band edges
  • the number of orbitals (states) per unit energy is called density of states, N(E) - the density of states is lower at the band edges
  • for some materials, the bonding and antibonding split giving an energy (band) gap - decreased orbital overlap = decreased energy gap
55
Q

Draw a diagram to describe insulators, semiconductors and metals using band theory.

A
  • Fermi level is the energy with a 50% probability of electron occupation under any conditions
56
Q

Show the bands formed in Be (hcp structure) and how they’re filled.

A
57
Q

Show the bands formed in diamond (C) and how they’re filled.

A
58
Q

Show the bands formed in Na (bcc structure) and how they’re filled.

A
59
Q

Show the bands formed in Cu (fcc structure) and how they’re filled.

A
60
Q

Describe the orbital dependency of conductivity.

A
  • electron delocalisation increases conductivity
  • orbital overlap, energy and shape are key
  • s-orbitals are isotropic = good delocalisation
  • heating a metal reduces orbital overlap and the ions vibrate more = decreases conductivity
61
Q

Describe the simple free electron model for a metal.

A
  • similar to ideal gas
  • electrons are able to move without interacting with the positive lattice or each other (Fermi gas)
  • can be used to estimate the Fermi energy (EF)
62
Q

Give the equation for the Fermi energy.

A
63
Q

Describe how temperature affects the occupancy of electrons in bands.

A
  • at 0 K - electrons are ‘paired’ in band orbitals
    • the highest filled energy at 0 K is the Fermi energy
  • above 0 K - electrons are promoted by heat to higher energy orbitals (increases conductivity)
    • the energy with a 50% chance of occupation is called the Fermi level
64
Q

Describe semiconductor doping.

A

Semiconductor doping modifies the conductivity and position of the Fermi level.

  • doping with a group 15 element givens an extra electron in an orbital with an energy within the band gap (n-doping)
  • doping with a group 13 elements gives one fewer electron in an orbital with an energy within the band gap (p-doping)
65
Q

Describe the temperature dependent conductivity of a doped semiconductor.

A
66
Q

Describe Fermi levels at the interface of any two substances

A
  • the Fermi levels will equilibrate (electrons are transferred)
  • an example is a p-n junction:
    • at the interface of a p-n junction, charge is transferred from n to p to equilibrate the fermi levels
    • charge transfer causes generation of a field in a region close to the interface
67
Q

What two properties do superconductors exhibit?

A
  1. below a critical temperature (Tc) zero electrical resistance is observed
  2. below Tc, magnetic flux is expelled B = 0 (Meissner effect) - χ = -1
68
Q

Describe the structure of cuprates.

A
  • there are two Cu sites: a distorted square pyramid of Jahn-teller distorted Cu2+ (that form CuO2 layers) and square planar geometry
  • oxygen is removed from the basal planes (0, 1/2, 0) leading to linear geometry for the Cu atoms linking the CuO2 layers
  • the structure is orthorhombic: a ≠ b ≠ c
69
Q

What are the important structural features of cuprates?

A
  • CuO2 square planar layers separated by ‘charge resevoir layers’ controlling the average Cu oxidation state in the CuO2 layers
  • the average Cu oxidation state should be > +2
70
Q

Describe fullerides.

A
  • synthesised by intercalation of electropositive metals into the C60 lattice
  • electron transfer from the metal to C60 gives C60n- anions (fullerides)
  • the orbitals of neighbouring C60 molecules overlap forming bands, and the electrons are able to move through the solid i.e. metallic
  • Tc is high
71
Q

Describe A3C60.

A
  • superconducting (A = alkali metal)
  • cubic structure
  • all the tetrahedral and octahedral sites are filled
  • Tc is proportional to the average cation volume (the distance between C60 molecules)
72
Q

Describe electron-phonon coupling.

A
  • electron-phonon coupling is the mechanism by which electrons can be attracted to each other
    • the two electrons are known collectively as a Cooper pair
  • the two electrons don’t need to be close to e/o
73
Q

Describe how the importance of phonons can be determined experimentally.

A
  • the frequencies of lattice vibrations can be quantised as phonons
  • can be demonstrated experimentally by the use of isotopes
  • Tc is inversely proportional to √M, M = mass of lattice ion
74
Q

Describe the electrostatics of electron-phonon coupling.

A
  • usually a repulsive electrostatic interaction between two electrons
  • electron-phonon coupling must be strong for the Cooper pair to remain intact and it must be greater than electron-electron repulsion
  • the binding energy of Cooper pairs is usually weak and that’s why Tc is usually low
75
Q

Describe the shapes of nanoparticles.

A
  • exhibit a range of shapes
  • each shape and surface has a unique energy and electronic structure
  • certain shapes are preferred thermodynamically
  • surface can have many defects
  • cubeoctahedron is very common
  • surfaces with low Miller indices have lower surface energy
76
Q

Describe how shape can be controlled by wet chemical methods.

A
  • used to prepare soluble nanoparticles
  • need to prevent aggregation which causes precipitation - coat the nanoparticle surface
  • ligands can form a steric barrier or cause electrostatic repulsion between particles
  • can use many different molecules which covalently bind to the metal or metal compound surface
  • size and shape of the nanoparticles can be controlled by synthesis temperature, time and relative concentrations of ligand and metal
77
Q

What are the different diffraction methods to analyse nanoparticles?

A
  1. x-ray diffraction
  2. neutron diffraction
  3. electron diffraction
78
Q

Describe x-ray diffraction of nanoparticles.

A

Maps electron density giving relative atomic positions.

79
Q

Describe neutron diffraction of nanoparticles.

A

Based on scattering length and cross sections of individual isotopes.

Neutrons also have a magnetic moment allowing the magnetic structure to be determined.

80
Q

Describe electron diffraction of nanoparticles.

A

Most often used in conjunction with electron microscopy. Sensitive to electron density similar to x-ray diffraction.

Can be used on individual nanocrystals.

81
Q

Describe how particle size can be obtained from x-ray diffraction.

A

The width of diffraction peaks increase as the size decreases, and is described by the Scherrer equation. Applicable to particles < 100 nm.

The calculated value does not include other effects of broadening, so it is often an underestimation.

82
Q

Why do we need electron microscopy?

A

To distinguish two positions you need sufficient resolving power. The minimum distance that can be resolved is described by the Abbe diffraction limit.

Shorter wavelength = smaller distance resolved.

High energy electrons have very small wavelengths and therefore can be used to image very small distances.

83
Q

What are the different modes of electron microscopy?

A

Probes structure and properties of materials.

  1. SEM - morphology and particle size distribution
  2. EDS - gives an element map
  3. TEM + STEM
  4. Electrom diffraction - crystal structure of individual particles
  5. EELS - element maps for lighter elements than EDS
84
Q

What are the different modes of scanning probe microscopy?

A

Probes structure and function.

  1. STM - maintains current between tip and sample
  2. AFM - measures deflection of tip as it scans across surface of sample
85
Q

Describe the electronic structure and optical properties of superconductors.

A
  • as the number of atoms and size reduces, the band structure tends toward that of a molecule
  • when a photon is absorbed, an excited state (electron-hole pair) called an exciton is generated
  • relaxation can lead to fluorescence which is size dependent
    • nanoparticles in this size regime are called quantum dots
  • the gap will increase with decreasing size
86
Q

Describe the electronic structure and optical properties of metals.

A
  • the conduction band is retained until very small particle size
  • the conduction electrons can absorb light leading to a collective excitation called surface plasmon resonance (SPR)
  • for some metals, SPR is in the visible region leading to colour
  • SPR is dependent of a number of factors such as size and shape

Core 9 (5 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions