Planes and Solid Figures

Question 1

Parametric

dy/dx = ?

d²y/dx² = ?

Answer 1

dy/dx = ^dy/dt/_dx/dt

d²y/dx² = ( u’v” – u”v’ ) / (u’)³

x = u, y = v

Question 2

Disk method

y = ƒ(x) revolved around x-axis on interval [a, b]

V = ?

Answer 2

V = π ∫_a^b ƒ(x)² dx

Question 3

Washer method

Region between y = ƒ(x) and y = g(x)

revolved around x-axis, on interval [a, b]

V = ?

Answer 3

V = π ∫_a^b [ƒ(x)² – g(x)²] dx

Question 4

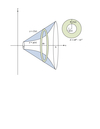
Cylindrical shells method

Region between y = ƒ(x) and y = g(x)

revolved around y-axis, on the interval [a, b]

h = ?

r = ?

V = ?

Answer 4

• h = ƒ(x) – g(x)
  
  • ​Or larger value – smaller value
• r = x
  
  • Or x – a, if rotated around x = a
  • Or Difference between x values
• V = 2π ∫_a^b x [ƒ(x) – g(x)] dx

Question 5

If a function has a critical value at x=c, then how do you tell whether it is a relative maximum or a relative minimum?

Answer 5

Relative maximum if ƒ”(c) < 0

Relative minimum if ƒ”(c) > 0

Question 6

How do you know when the curve is concave up, concave down, or at a point of inflection?

Answer 6

When ƒ”(x) > 0, the curve is concave up.

When ƒ”(x) < 0, the curve is concave down.

When ƒ”(x) = 0, the curve is at a point of inflection.

Question 7

Arc Length

L = ∫_a^b dL

Answer 7

L = ∫_{<span>a</span>}^{<span>b</span>} √ ( 1 + ƒ’(x)^{<span>2</span>} ) dx

dL = √( dx² + dy² )

for parametrics

Question 8

Area of a surface of revolution

S = ?

dL = ?

Answer 8

S = 2π ∫_a^b r dL

dL = √( dx² + dy² )

dL = √ ( 1 + ƒ’(x)² ) dx

Question 9

Polar coordinates

Area of region = ?

Length of curve = ?

Answer 9

A = ∫_a^b ( 1/2 r² ) dø

L = ∫_a^b √( (dr/dø)² + r² ) dø