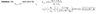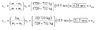Physics Exam 2: Chapters 6-11 Flashcards
(51 cards)
1
Q
A
1
Q
A
Linear Speed: 2pi(d)/t
1
Q
A
1
Q
A
2
Q
A
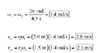
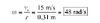
w2=wo2+2aØ
2
Q
A
3
Q
A
4
Q
A
5
Q
A
7
Q
A
8
Q
A
9
Q
A
9
Q
A
10
Q
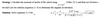
torque= Ia
I= mr2
A
11
Q
A
11
Q
A
12
Q
A
13
Q
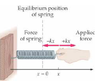
When a block is on top of a verticle spring, the spring compressed 0.0315m. Find the mass of the block given that the force constant of the spring is 1750N.
A
F= kx
F=mg
kx=mg
m= kx/g
m= (1750)(0.0315)/(9.8)
m= 5.62kg
15
Q
Two blocks are connected by a string. The smooth inclined surface makes an angle of 42º with the horizontal, and the block on the incline has a mass off 6.7kg. Find the mass of the hanging block that will cause the system to be in equillibrium.
A
Fx= T- (M)(g)sin(Ø)= 0
T= (m)(g) = (M)(g)sin(Ø)
(m) (g)=(M)(g)sin(Ø) (gravity cancels)
(m) = (M)sin(Ø)
(m) = (6.7)sin(42)
m= 4.48kg
16
Q
How do you decrease centripetal acceleration for jet pilots?
A
17
Q
Find the acceleration of the masses shown
m1= 1kg
m2= 2kg
m3= 3kg
A
£F=(m)(a)
(m3 is the only block experiencing real gravity)
(m1+m2+m3)(a)=(m3)(g)
a= (m3)(g)
(m1+m2+m3)
a= (3)(9.81)
(1+2+3)
a= 4.9 m/s2
17
Q
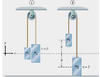
Find the direction and the magnitude of the hanging blocks acceleration if its mass is 4.2kg
What we know
M= 5.7kg
m=4.2kg
A
Parallel: (m)(g)sin(Ø)
Tension=(m)(g)
£F= (m)(a)
-(M1)(g)sin(35)-T=(m2)a
T= -(M1)(g)sin(35)-(m2)a
£F=ma
[(M1)(a)sin(35)-(m2)g]+ mg = (M1+m2)(a)
a=
a=
17
Q
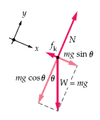
At the airport, you pull a 18kg suitcase across the floor with a strap at a 45º angle above the horizontal. Find the normal force and the tension in the strap, givn that the suitcase moves with constant speed and the coefficient of kinetic friction between the suitcase and the floor is 0.38.
A
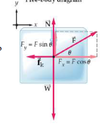
T= 68.69
18
Q
Find the coefficient of kinetic friction between a 3.85kg block and the horizontal surface on which it rests if a 85N spring must be stretched by 0.062m to pull it with constant speed. Assume spring is pulled in horizontal direction.
A
Ff = kx
Ff= (85N)(0.062m)= 5.27
Fn= mg
Fn= (3.85kg)(9.81m/s2)= 37.73
u=Ff/Fn
u= (5.27)/(37.73)
u= 0.14
20
Suppose mass 1 and mass 2 increase by 1 kg, does the acceleration stay the same?
The acceleration of the blocks would decrease since the denominater of the base increased
22
A child goes down a slide with an acceleration of 1.26 m/s^2. Find the coefficient of kinetic friction between the child and the slide if the inclined plane is 33º below the x-axis.
Parallel Axis: (m)(g)sin(33º)
Friction: (m)(g)cos(33º)u
£F=ma
(m)(g)sin(33º)-(m)(g)cos(33º)µ=(m)(a)
(mass cancels)
u= _(a)-(g)sin(33)_
-(g)cos(33)
u= _(1.26)- (9.81)sin(33)_
-(9.81)cos(33)
**u= 0.496**
24
A spring with a force constant of 3.5 x 104 N/m is initially at its equillibrium length. How much work must you do to stretch the spring 0.05m? How much work must you do to compress it 0.05m?
F=kx
Wspring= (1/2)(k)(x)2
k= 3.5x 104
x= 0.05m
F= kx
Wspring= (1/2)(k)(x)2
Wspring= 43.75
25
A farmer pushes a 26kg bale of hay 3.9m across the floor of a barn. If she exerts a horizontal force of 38N on the hay, how much work has she done?
W=(Fd)cos(Ø)
F=88N
d= 3.9m
FLAT: cos(0)= 1
W= (Fd)cos(Ø)
W=(88)(3.9)cos(0)
**W= 343.2 J \> 34.32 KJ**
26
The international space stationorbit the Earth in an approximately circular orbit at a height of h=375 km above the Earths surface. In one complete, is the work done by the Earth or the space station positive, negative, or zero?
Since the space station remains in a stead circular orbit, the work done by the Earth is zero.
26
How much work is needed for a 73 kg runner to accelerate from rest to 7.7m/s?
W= KE
KE= (1/2)(m)(v)2
Since we are given velocity...
W=KE
W= (1/2)(73)(7.7)2
**W= 2164.1J \> 2.164KJ**
26
A 0.14kg pinecone falls 16m to the ground, where it lands with a speed of 13m/s. Whith what speed would the pinecone have landed if there had been no air resistance? Did air resisitance do positive work, negative work,or zero work on the pincone?
PE= mgh
KE= (1/2)(m)(v)2
W= Ui-Uf
To find air reistence: W= PE-KE
Potential Energy to Kinetic Energy
W= mgh-(1/2)(m)(v)2
W= (0.14)(9.81)(16)- (1/2)(0.14)(13)2
**W= -10.14** (Air resistence is negative)
No Air Resistence: Ui=Uf
mgh=(1/2)(m)(v)2 (mass cancels)
v2=(2)(g)(h) \> v= sqrt(2)(g)(h)
**Vf = 17.70 m/s**
Faverage = 10.1/17.7
**Favareage= 0.57**
27
An ice cube is placed in a microwave oven. Suppose theoven delivers 105W of power to the ice cube and that it takes 32,200J to melt it. How long does it take for the ice cube to melt?
Energy Lost= Energy Gained
Power= Work/Time
Power= Work/Time
Time= Work/Power
Time= 32200J/105W
Time= 306.66sec
29
A 9.50 bullet has a speed of 1.30 km/s. What is its kinetic energy in joules? What is the bullet's kinetic energy if its speed is halved? If it is doubled?
v= 1.30km/s\> v= 1300m/s
KE= (1/2)(m)(v)2
mbullet=9.50g\> mbullet= 0.0095kg
KE= (1/2)(m)(v)2
KE= (1/2)(0.0095)(1300)2 = 8026J \> 8.026K
KE= (1/2)(0.0095)(650)2 = 2007J \> 2.007KJ
KE= (1/2)(0.0095)(2600)2 = 32110J \> 32.11KJ
30
A 51kg packing crate is pulled with constant speed across a rough floor with a rope that is at an angle of 43.3º above the horizonal. If the tension in the rope is 115N, how much work is done on the crate to move it 8m?
W= FdcosØ
W= FdcosØ
W= (115)(8)cos(45)
W= 669.55J \> 0.67KJ
32
The 2 masses in the Atwoods machine are initially at rest at the same height. After they are released, the large m2 falls through a height h and hits the floor, and the small m1 rises at the same height h. Find the speed of the masses just before m2 lands giving your answers in terms of m1, m2, g, and h. Evaluate your answer to part a, for the case...
h= 1.2m
m1= 3.7kg
m2= 4.1kg
KE+PE=KE+PE
KE+PE= KE+ PE
Since vi is 0 and no PE at the end
mghi= (1/2)mv2
(M2-m1)gh= (1/2)(M2+m1)(vf)2
Vf= sqrt(2)(M2-m1)(g)(h)/(M2+m1)
Vf= sqrt(2)(4.1-3.7)(9.8)(1.2)/(4.1+3.7)
**Vf= 1.12m/s**
34
A player passed a 0.6kg basketball downcourt for a fast break. The ball leaves the players hands with a speed of 8.30m/s and slows down to 7.1m/s at it highest point. Ignoring air resistence, how much high above the release point is the ball when it is at its maximum height. How would doubling the mass of the ball affect the result in Part A?
KE+PE=KE+PE
m= 0.60kg
Vi= 8.30 m/s
Vf= 7.1 m/s
KEi + mghi = KEf + mghf (no inital PE enegy)
(1/2)(m)(vi)2= (m)(g)(h) + (1/2)(m)(vf)2
h = (1/2)(vi)2- (1/2)(vf)2/ (g)
h= (1/2)(8.30)2-(1/2)(7.1)2/ (9.81)
**h= 0.94m**
**Doubling the mass would not change anything since mass cancels in this problem**
35
In a tennis match, player wins a point by hitting the ball sharply to the ground. If the ball bounces upward from the ground with a speed of 16m/s, and i caught by a fan in the stands with a speed of 12m/s, how high above the court is the fan? Ignore air resistence. Explain why it is not necessary to know the mass of the tennis ball.
PE+KE = PE+KE
Vi= 16 m/s
Vf= 12 m/s
PEi+KEi=PEf+KEf
No PEi \> KEi= PEf + KEf
(1/2)mvi2 = mghf + (1/2)mvf2 (mass cancels)
hf= (1/2)(vi)2- (1/2)(vf)2/(g)
hf= (1/2)(16)2- (1/2)(12)2/ (9.81)
**hf= 5.7m**
**Mass cancels out which is why it is not used**
36
A 1.75kg block at rest on a ramp of height h is released and slides without friction to the bottom of the ramp, and then continues across a surface that is frictionless except for a rough patch of width of 0.01m that has a coefficient of kinetic friction uk=0.640. Find h such that the blocks speed after crossing the rough patch is 3.5 m/s.
m= 1.75kg
Rough Patch= 0.01
uk= 0.640
Vf= 3.5m/s
h=?
With Friction:
Wnc= -mg(uk)d
-mg(uk)d= (1/2)(m)(vf)2- (m)(g)(h) (masses cancel)
h= (g)(uk)d+(1/2)(vf)2/(g)
h= (9.81)(0.640)(0.01)+(1/2)(3.5)2/ (9.8)
**h= 0.68m**
37
Catching a wave, a 77kg surfer starts with a speed of 1.3 m/s drops through a height of 1.65m, and ends with a speed of 8.2m/s. How much non-conservative work was done on the surfer?
PE+KE = PE+KE
W= Initial- Final
h=1.65m
m= 77kg
Vi= 1.3m/s
Vf= 8.2m/s
Wnc= ?
PEi+KEi= PEf + KEf
(No PEf) so PEi +KEi= KEf
Wnc= PEi+KEi-KEf
Wnc= (77)(9.8)(1.65) + (1/2)(77)(1.3)2-(1/2)(77)(8.2)2
**Wnc= -1278.58J**
38
A 42kg seal at an amusment park slides from rest down a ramp into the pool below. The top of the ramp is 1.75m higher than the surface of the water, and the ramp is inclined at an angle of 35º above the horizontal. If the seal reaches the water with a speed of 4.40m/s, what is the work done by kinetic friction? What is the coefficient of kinetic friction between the steel and the ramp?
m= 42kg
h= 1.75
vi= 0m/s
vf=4.40m/s
Wnc= PEi+KEi - PEf+KEf
Friction: u(m)(g)cos(Ø)d
At the Top:
PE= mgh
(42)(9.81)(1.75)
PE= 720.3
At the Bottom:
KE= (1/2)(m)(v)2
(1/2)(42)(4.40)2
KE= 406.56
Wnc=PEi-KEf
Wnc= 720.3 - 406.56
**Wnc= 313.75**
Wnc= mgcosØ(u)d
313.75= mgcosØ(u)d
u= 313.75/mgcosØd
u= 313.75/(42)(9.81)cos(35º)(1.75)
**u= 0.304**
39
A 2.9kg block slides with a speed of 1.6m/s on a frictionless horizontal surface until it encounters a spring. If the block compresses the spring 0.048m before coming to rest, what is the force constant (k) of the spring? What initial speed should the block have to compress the spring by 0.0012m?
Vf= 1.6m/s
x= 0.048
Vi= ?
k= ?
(1/2)(m)(v)2 = (1/2)(k)(x)2
Kinetic Energy = Spring Energy
(1/2)(m)(vf)2 = (1/2)(k)(x)2
K= (2)(1/2)(m)(Vf)2/ (x)2
K= (2)(1/2)(2.9)(1.6)2/ (0.0048)2
**K= 3,222**
Finding Vi
(2)(1/2)(m)(vi)2= (1/2)(k)(x)2
Vi= sqrt(k)(x)2/(m)
Vi= sqrt(3222)(0.012)2/ (2.9)
**Vi= 0.16m/s**
40
As a cliff diver drops to the water from a height of 46m, his gravitational potential energy decreases by 25,000J. What is the divers weight in Newtons?
Energy Gained= Energy Lost
PE= mgh
Energy Gained= Energy Lost
PE= 25,000J
mgh= 25,000J
m= 25,000J/ (g)(h)
**m= 55.45kg \> 0.554kN**
42
Two ice skaters stand at rest in the center of an ice rink. When they push off each other, the 45kg skater acquires a speed of 0.62 m/s. If the speed of the outer skater is 0.89m/s, what is this skaters mass?
mv=mv
Skater 1: 45kg going 0.62m/s
Skater 2: ?kg going 0.89m/s
mv=mv
(m1+m2)vi= (m1v1) + (m1v1)
vi= 0m/s
0= (45)(0.62)+(m2)(0.89)
m2= (45x0.62)/(0.89)
**m2= -31.35 (Going in the opposite direction relative to the other skater)**
43
The collision between a hammer and a nail can be considered elastic. Calculate the KE acquired by a 0.012kg nail stucked by a 0.55kg hammer movingwith an initial speed of 4.5 m/s.
44
A 72.5kg tourist climbs up the stairs to the top of the Washington Monument which is 55ft (209m). How far does the Earth move in the opposite direction as the tourist climbs?
45
Two air-track carts move toward eachother on an airtrack. Cart 1 has a mass of 0.35kg and a speed of 1.2m/s. Cart 2 has a mass of 0.61kg. What speed must cart 2 have of the total momentum of the system is to be 0? Since the momentum of the system is 0, does it follow that the kinetic energy of the system is also 0? Verify your answer to part B by calculating the systems kinetic energy.
P=mv
Cart 1= 0.35kg going 1.2
Cart 2= 0.61kg going ?
mv=mv (when momentum is 0)
When momentum is zero: m1v1=m2v2
v2= (m1)(v1)/(m2)
v2= (0.35kg)(1.2m/s)/(0.61kg)
**v2=** **0.69m/s**
KE Cart 1: (1/2)(0.35)(1.2)2
**KE Cart 1= 0.252J**
KE Cart 2: (1/2)(0.61)(0.69)2
**KE= 0.145J**
**No, it does not follow that when momentum is 0, KE is 0**
46
Find the magnitude of the impulse delivered to a soccer ball when a player kicks it with a force of 1250N. Assume that the players foot is in contact with the ball for 0.00595 seconds.
Impulse= Force x Time
F= 1250N
t= 0.00595 seconds
Impulse= Force x Time
Impulse= 1250N x 0.00595 sec
**Impulse= 7.44 kgxm/s2**
47
A 732kg car stopped at an intersection is rear ended by a 1720kg truck moving with a speed of 15.5m/s. If the car was in neutral and its breaks were off so that the collision is elastic, find the final speeds of both vehicles after the collision.
Car Before: 732kg going 0m/s
Truck Before: 1720kg going 15.5m/s
Car and Truck Speed After?
Initial=Final
(v1=0m/s) m1v1+ m2v2 = (m1+m2)vfinal
Vfinal= (m2v2initial) / (m1+m2)
Vfinal= (1720x15.5m/s) / (732+1720)
**Vfinal= 10.87m/s (inelastic)**
48
A bullet with a mass of 0.004kg and a speed of 650 m/s is fired at a block of wood with a mass of 0.095kg. The block rests on a frictionless surface, and is thin enough that the bullet passes completely through it. Immedietly after the bullet exits the block, the speed of the block is 23m/s. What is the speed of the bullet when it exits the block? Is the final KE of the system equal to, less than, or greater than than the initial KE?
Bullet Before: 0.004kg going 650 m/s
Block Before: 0.095 going 0m/s
Block after: 0.095 going 23m/s
Bullet after: 0.004kg going ?m/s
Initial=Final
m1v1+m2v2= m1**v1**+m2v2
V1final= [(m1)(v1)initial+m2(v2)initial]- [m2v2final]/(m1)
V1final= [(0.004x650)+(0.095x0)]- [0.095x23]/(0.004)
**V1final= 103.75 m/s**
KE of Bullet and Block Before:
(1/2)(0.004)(650)2+ 0= **845J**
KE of Bullet and Block After:
(1/2)(0.004)(103.75)2+ (1/2)(0.095)(23)2= **47J**
50
An object initially at rest breaks into 2 pieces as the result of an explosion. One piece has twice the kinetic energy of the other piece. What is the ratio of the masses of the 2 pieces? Which piece has the larger mass?
51
A carboard box is in the shape of a cube with each side of length L. If the top of the box is missing, where is the center of mass of the open box? Give answer relative to geometric center of the box.
