Final Exam: Chapters 12+13

Question 1

For gravity: F= ?

G= ?

Answer 1

F= (G) m1m2/R²

G= 6.67 x10^-11

Question 2

m1= 1000kg

m2= 1000kg

Distance= 5m

What is the force between the 2 cars with the law of gravity?

Answer 2

G= (m1)(m2)/R²

G= (6.67_E^-11)(1000)(1000)/(5²)

G= 2.67 x10^-6N OR 2.67uN

Question 3

Is light affected by gravity?

Answer 3

Yes, because light bends around objects. It actually deals with 4-Dimensions.

Question 4

F= (G) (m1xm2)/R²

Only Answer This One:

Find the force of gravity between the Earth and Moon.

F= (G) (m_{moon X} M_Earth)/ (R²)

Earth and Sun:

Just Practice: F= (G)(m_EarthxM_Sun)/(R²)

Answer 4

Earth and One

F= (6.67E--11)(7.36E22)(5.98E24)/(385,000,000)2

F= 1.98_E²⁰N

Tidal forces are bigger between the Earth and the Sun in order to keep the Earth in orbit.

Question 5

How did we get 9.81 as the acceleration for gravity?

F= (G)(m1M2)/(R²)

mg= (G) (m1M2)/(R²) (small m’s cancel)

g= (G) (M2)/(R²)

Turns Into:

g= GM/R^{2 (cause little m’s canceled out)}

G= 6.67_E^-11

M= 5.98_E²⁴

^{m= Doesn’t Matter (Cancels)}

R= 6,378,000

Answer 5

g = (6.67_E^-11)(5.98_E²⁴)/ (6,378,000²)

g= 9.85 m/sec²

^{(Depends where you are on the Earth)}

Question 6

g= 9.8 m/sec²

If a person standing on the equater weigh less than someone who is somewhere else on the Earth?

Answer 6

Person: (G)(mM)/(R²)

F_c= (m)(v²)/(R)

F_G= (G)(mM)/(R²)

Apparent Weight:

Apparent Weight= [(G)(mM)/(R²)] - [(m)(v²)/(R)]

V= D/T

V= (40,000m/86,164sec)

V= 464.23 m/s

[(6.67_E^-11)(80)(5.98_E²⁴)/(6,378²)] - [(80)(464.23²⁾/(6,378)]

784.4- 2.7

Apparent Weight= 781.7 Newtons

Percent Difference: (2.7/784.4) X 100% = 0.34% less at the Equater

Question 7

Acceleration between a Satellite and the Earth?

Satellite: 1000kg

Satellite height from Earth: 500,000m

F= G(mM)/(R²)

F= ma

F= (G)(mM)/(R_Earth+R_Satellte)²

Answer 7

ma= (G)(mM)/(R_Earth + R_Satellite)²

a= (G)(M)/(R_Earth + R_Satellite²)

a= (6.67_E^-11)(5.98_E²⁴)/ (6,378,000+ 500,000)²

a= 8.43 m/s²

Question 8

Find M

a_c= 2.03 m/sec²

R= 250,000,000m

a_c= (m)(v²)/(R)

F= (G) (mM)/(R²)

F= ma_c

(G)(mM)/(R²)= ma_c (little mass cancels)

(G)(M)/(R²)= ac

Find the Mass (M)

Answer 8

M= (a_c)(R²)/(G)

M= (2.03)(250,000,000)²/(6.67_E^-11)

M= 1.90x10²⁷kg

^Mass of Jupitor!

Question 9

How to Find the Mass of the Earth:

a= g= 9.81m/sec²

G= 6.67_E¹¹

Distance: 6,378m

F_g=F_G

mg= (G)(mM)/(R)² (small masses cancel)

M= (g)(R²)/(G)

M= (9.81)(6,378²)/(6.67_E^-11)

Density= M/V

p=M/V

Answer 9

M= 5.98_E²⁴kg

p= M/V

Density is higher in the middle of an object

Question 10

Finding the Density of the Earth

Finding Big M and putting it in the Density Equation of a SPHERE

a=g= 9.81m/sec²

Density= Mass/Volume

p= m/v

F_G=F_g

mg= (G)(mM)/(R²) (small masses cancel)

M=

Answer 10

mg= (G)(mM)/(R²) (small masses cancel)

M= (g)(R²) / (G)

M= (9.81)(6,378²)/(6.67_E^-11)

M= 5.98_E²⁴

p= M/V

Volume of a Sphere: (4/3)π(R³)

p= 5.98_E²⁴/ (4/3)π(6,378³)

p= 5,500 kg/m³

Question 11

Keppler’s First Law:

Answer 11

R1+R2 = 2a

(2a: Semi-major axis)
(2b: Semi-minor axis)

R=R1=R2

R1+R2=2a

2R=2a

R=a

a²+b²= c²

Question 12

Eccentricity of a Planet’s Orbit

Eccentricity (e) = c/a

R_p= 147,098,000m

R_A= 152,098,000m

e= R_a-R_p/ R_a+R_p

e= 152,098,000 - 147,098,000 / (152,098,000 + 147,098,000)

e= 0.0167

Answer 12

e= R_a-R_p/ R_a+R_p

e= 152,098,000 - 147,098,000 / (152,098,000 + 147,098,000)

e= 0.0167

R_p+R_a=2a

_{<span>R</span>p}= a-c

R_a= a+c

e= R_a-R_a/ R_a+R_p

e= [a+c] - [a-c] / [a+c] + [a-c]

e= 2c/2a

e=c/a

Question 13

Keppler’s Second Law:

L= r x mv = mr x v

Torque: L/T = 0

Torque= rFsinØ = rFsin(180º) = 0

Answer 13

Question 14

Kepplers 3rd Law:

T²= R²

F_G= F_c

(G)(mM)/(R²) = mv²/R (small masses cancel and 1 R)

V²= (G)(M) / (R)

V= Distance/Time

v²= e= Ra-Rp/ Ra+Rp

V= D/T

v= 2πR/T

v²= 4π²R²/T²

4π²R²/T² = (G)(M) / (R)

Answer 14

Question 15

How To Find Orbital Velocity:

F_G= F_c

(G)(mM) / (R²) = mv² / (R) (small mass cancels)

v= sqrt[(G)(M)/(R)]

v= sqrt[(6.67_E^-11)(5.98_E²⁴) / (6,378,000)]

v= 7,908 m/s

Answer 15

Vorbit⁼ sqrt (G)(M)/ REarth + h)

V_orbit= sqrt[(6.67_E^-11)(5.98_E²⁴) / (6,378,000)]

v= 7,615 m/sec

v= Distance/Time

Time= Distance/Velocity

Time = 2π(R_Earth +h)/ (v)

= 2π(6,876,000m) / (7,615 m/sec)

= 5,675 sec

Question 16

Orbital Velocity: Find the distance

V_orbit= sqrt[ (G)(M) / (REarth + h)

V= Distance/Time

v= 2πR / T

[2π(R_h + h)²/T^{2] = [}(G)(M)/ R_{Earth +} h]

[4π²R²/ T²] = [(G)(M) / (R)]

R³= [GMT²/ 4π²]

R= sqrt3 [GMT²/ 4π²]

R= sqrt3 [(6.67_E^-11)(5.98_E²⁴)(86,164sec)²/ 4π²]

R= 43, 172km or 26,210m/s

Answer 16

Question 17

Gravitational Potential Energy:

PE= mgh

W= Fd

W= GmM/R₁ - 0

Answer 17

PE_Gravity at R1= [(6.67_E^-11)(1000)(5.98_E²⁴)/ 6,378,000]

PE_Gavity= 6.25_E¹⁰J

Question 18

Answer 18

Just review

Question 19

Kinetic and Potential Energy In Orbit

E_total= PE + KE (potential energy is usually negative)

E_total= [-(G)(M)(m) / (R_{Earth +} R_Satellite)] + [(1/2)(m)(GM/R)]

PE: [-(6.67_E^-11)(1000)(5.98E²⁴) / (6,378,000 + 500,000)

PE= -5.8_E¹⁰J

KE= (1/2)(m)(v²)

KE_Orbit= (1/2)(m)(GM/R)

KEOrbit= 2.9_E¹⁰

E_total= KE - PE

E_total= (2.9E¹⁰+ (-5.8_E¹⁰)

E_Total= -2.9E¹⁰J

Answer 19

Question 20

Answer 20

Just Review

Question 21

Answer 21

Review

Question 22

Ceres, the largest asteroid known, has a mass of roughly 8.7_E²⁰kg. If Ceres passes within 14,000,000m of the spaceship in which you are traveling, what force does it exert on you?

Mass of spaceship: 70kg

Answer 22

F= (G)(mM)/(R²)

F= (6.67_E^-11)(8.7_E²⁰)(70kg)/ (14_E6²)

F= 0.0207

Question 23

At what altitude above the Earth’s surface is the acceleration due to gravity equal to (g/2)?

Answer 23

When a space station satellite is at a certain height from the Earth:

[GM_Earth / (R_Earth + h)2] = [(1/2)(Gm_Satellite) / (R²)]

(R_Earth + h)² = 2R²_Satellite

h= ((sqrt2) - 1)R_{Earth =} ((sqrt2) - 1)(6.67_E⁶)

h= 2.64_E6m

Question 24

The acceleration due to gravity on the Moon’s surface is known to be about (1/6) the acceleration due to gravity on the Earth. Given that the radius of the Moon is roughly (1/4) that of the Earth, find the mass of the Moon in terms of the mass of the Earth.

Answer 24

Question 25

Two Satellites orbit the Earth, with satellite 1 at a greater altitude than satellite 2. **A.)** Which satellite has the greater orbital speed? **B.)** Calculate the orbital speed of a satellite that orbits at an altitude of one Earth radius above the surface of the Earth. **C.)** Calculate the orbital speed of a satellite that orbits at an altitude of two Earth radii above the surface of the Earth.

Answer 25

Question 26

Find the minimum KE needed for a 39,000kg rocket to escape **A.)** At the moon or **B.)** The Earth.

Answer 26

Question 27

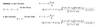
Suppose one of the Global Positioning System satellites has a speed of 4.46m/sec at perigee and a speed of 3.64km/sec at apogee. If the distance from the center of the Earth to the Satellite at perigee is 2.00_E⁴km, what is the corresponding distance apogee?

Answer 27

Question 28

If a projectile is launched vertically from the Earth with a speed equal to the escape speed, how high above the Earth's surface is it when it's speed is half the escape speed?

Answer 28

Question 29

E_Ocillation= PE + KE Translates to... Find the velocity formula Find the acceleration formula

Answer 29

(1/2)ka² = (1/2)kx² + (1/2)mv² (the 1/2 cancels) ka² = kx² + mv² v²= (ka²- kx²) / (m) (can factor out k) **v = sqrt(k(a²-x²)) / (m))** Finding acceleration: F= -kx F=ma -kx = ma **a= (-kx) / (m)**

Question 30

Simple Harmonic Motion in Terms of Time X as a function of time? V as a function of time? a as a function of time? X = Acos (wt + Ø) Compressed: X = -a Stretched: X= a Ø= wt

Answer 30

At position t= 0 (then Ø cancels) X= Acos (wt+Ø) **X as a Function of time: _X(t)= Acos (wt)_** **V as a function of time: _V(t)= -Awsin(wt)_** **a as a function of time: _a(t)= -Aw²cos(wt)_** **_[w= sqrt(k/m)] \> [w²= k/m]_**

Question 31

V at equillibrium point? V at x= 10cm? V at x=5cm? a at x=5cm? **Info:** **k= 1500** **A= 0.10m** **m= 4.2kg** E₀=E_f (1/2)kA²= (1/2)kx²+(1/2)mv²

Answer 31

mv²= kA²- kx² V²= (k/m) [A²-x²) V= sqrt[(k/m)(A²-X²)] (x becomes 0) **Part A:** v(x=0) = sqrt [(k/m)(A²)] V= sqrt [(1500/2.4)(0.1²)] **Part A: V(x=0)= +/- 1.89 m/sec** **Part B: V(x=0.1)= 0 (At max elongation 0.1)** **Part C:** V(x=0.5)= +/-sqrt [(k/m)(A²- (0.05²)] = +/-sqrt[(1500/4.2)(0.1²)-(0.05²)] **V= +/- 1.64 m/sec** **Part D:** F= -kx F= ma -kx=ma a= -kx/m a= [(-1500)(0.05)/(4.2)] **a= -17.86m/sec²**

Question 32

A.) Find the total energy B.) Find the maximum Amplitude C.) Find the V_Max K= 300N/M m= 0.15kg\V= 0.30 m/sec x= 0.012m

Answer 32

**Part A: Total Energy** E_Total= PE + KE E_Total= (1/2)kx²+ (1/2)(m)(v²) E_Total= (1/2)(300)(0.012²) + (1/2)(0.15)(0.3²) **E_Total= 0.02835J (Anywhere along the ocillation)** **Part B: Amplitude** V= sqrt [(k/m)(A²-x²)] V²= [(k/m)(A²-x²)] (V²m/k)= A²-x² A= sqrt [(V²m/k)+(x²)] A= sqrt[(0.3²x0.15/(300)) +(0.012²)] **Amplitude= 0.0137m** **Part C:** Vmax= When X=0 Vmax= sqrt[(k/m)(A²-0²)] Vmax= sqrt[(300/0.15)(0.0137²)] **Vmax= 0.61m/sec**

Question 33

A.) What is t when x=-5cm? B.) What is t when x= 2cm? C.) What is V when t= 1 sec D.) What is a when t=0.15 **Info:** A= 5cm f= 20Hz t= 1/f \> t= 1/20hz **t= 0.0375 sec**

Answer 33

Part A: t(x=5cm)= (3/4)T t(x=5cm)= (3/4)(0.05sec) **t(x=-5cm)= 0.0375sec** Part B: x(t)= Acoswt (can't use when t=0) **x(t)= Asinwt (when t=0 so USE THIS ONE)** wt= sin^-1(x/A) t= (1/w)sin^-1(x/A) w= 2πf t= (1/(2π x 20Hz))sin^-1(2/5) **t= 0.00327sec** **Part C:** V(t=1sec)= Awcoswt v(t=1sec)= (.05)(2π)(20Hz) cos[(2π)(20Hz)(1sec) **V(t=1 sec)= 6.28 m/sec** **Part D:** a= -Aw²sinwt a(t=0.15)= (0.05)(2π²)(20²) **a(t=0.15)= 0.00327**

Question 34

A person in a rocking chair completes 12 cycles in 21 seconds. What is the period and frequency of the rocking? T= (t/n) f= (1/T)

Answer 34

**Part A: Period** T= (t/n) T= (21sec/12cycles) **T= 1.75sec** **Part B: Frequency** f= (1/T) f= (1/1.75sec) **f= 0.57Hz**

Question 35

The position of a mass ocillating on a spring is given by x=(3.2cm)cos(2πt / (0.58sec). **A.)** What is the period of the motion? **B.)** What is the first time the mass is at the position x=0?

Answer 35

T= 0.58 sec x= (3.2cm) Given: cos(2πt / (0.58sec) cos[(2π/T)(t)] = cos [(2π/0.58)(t)] (A cosine function is zero at (1/4) and (3/4) of a period) t= (1/4)(0.58sec) **t= 0.15sec**

Question 36

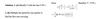
A mass oscillates on a spring with a period of 0.73 sec and an amplitude of 5.4cm. Write an equation giving x as a function of time, assuming the mass starts at x= A at time t=0

Answer 36

A= 5.4cm w= (2π/T) = (2π/0.73sec) **w= 8.6 rad/sec** x= Acosw x= (5.4)cos(8.6)t

Question 37

An object executing simple harmonic motion has a maximum speed Vmax and a maximum acceleration a_max . Find a.) the amplitude and b.) the period of this motion. Express answers in v_max and a_max.

Answer 37

Vmax= Aw a_max= Aw² A= (Aw)²/ (Aw)² A= (a_max/v_max) T= (2π/w) T= (2π) / (a_max/v_max) **T= 2πv_max / a_max**

Question 38

A 0.46kg mass attached to a spring undergoes simple harmonic motion with a period of 0.77 s. What is the force constant of the spring?

Answer 38

Question 39

A 0.40kg mass attached to a spring with a force contant of 26 N/m and released from rest a distance of 3.2cm from the equillibrium position of the spring. **a.)** Give the strategy that allows you to find the speed of the mass when it is halfway to the equilibrium position. **b.)** Use your strategy to find this speed.

Answer 39

Question 40

What is the maximum speed of the mass in the previous problem? How far is the mass from the equillibrium position when its speed is half the maximum speed?

Answer 40

Question 41

A simple pendulum of length 2.5m makes 5.0 complete swings in 16 seconds. What is the acce;eration of gravity at the location of the pendulum?

Answer 41

Question 42

Suspended from the ceiling of an elevator is a simple pedulum length of L. What is the period of the pendulum is the elevator **a.)** accelerates upward with an acceleration or **b.)** accelerates downward with an accaeleration whose magnitude is greater than zero, but less than g? Give your answer in terms of I,g, and a.

Answer 42