Partial differential equations Flashcards
(14 cards)
Define an ordinary differential equation
An ordinary differential equation is one in which the unknown function is a function of only one variable eg:
Define a partial differential equation
A partial differential equation is one in which the function is a function of more than one variable
Note: it is important to note whether or not these variables are independent of one another. If not, it is necessary to write which one is to be held constant
Define the order of a differential equation
The order of a DE is the order of the highest derivative
Define a linear differential equation
A D.E is linear if the unknown function does not appear in any power higher than 1
Define a homogeneous differential equation
A linear differential equation is homogeneous if all the terms depend on the unknown function or its derivatives. For the example below, the DE is homogeneous if G(x) = 0
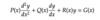
Define an inhomogeneous differential equation
A linear differential equation is inhomogeneous if not all the terms depend on the unknown function or its derivatives. For the example below, the DE is homogeneous if G(x) =/= 0
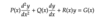
Define the degree of a differential equation
Describe the method of separation of variables
- The aim of separating a differential equation with n variables is to form n separate differential equations.
- For a DE with 2 variables x,y we can set u(x,y) = X(x)Y(y) and substitute this into the original equation.
- We can then change the partial derivatives into ordinary differentials as X and Y only depend on one variable each.
- Divide through by XY and rearrange to get X on one side and Y on the other
- x and y are independent variables so the separate DEs must both equal the same consant


