Ordinary differential equations

Question 1

Define a linear ODE

Answer 1

An ODE is linear if the dependent variable occurs at most to the first power.

Question 2

Define a homogeneous ODE

Answer 2

A linear ODE is homogeneous if the dependent variable appears to the first power in every term.

For the general form shown below, b(x) must = 0

Question 3

Describe how to determine whether or not an ODE is separable

Answer 3

Split dy/dx into dy and dx. If the ODE can be separated such that dy and all quantities containing y are on the left and dx and all quantities containing x are on the right, then the ODE is separable.

Question 4

Describe how to find the general solution of a separable ODE

Answer 4

Integrate the two sides of the equation by their respective variable.

Question 5

Describe the integrating factor method of solving a linear first-order ODE

Answer 5

S(x) denotes an integrating factor: S(x) = e^∫P(x)dx where P is described below in the equation for the standard form of a linear first order ODE.

Multiply all terms by S(x) and integrate both sides to determine an expression for the dependent variable.

Question 6

Describe the Perfect differential method (also known as the exact differential method) for solving a first order ODE

Answer 6

For an ODE that can be written as P(x,y)dx + Q(x,y)dy = 0, P and Q can be written as they are below.

Find a function f such that f(x,y) = C

Question 7

Give the necessary condition for P and Q to satisfy in order for the exact differential method to be relevant

Answer 7

Question 8

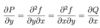
Give the standard form of a second-order linear ODE with constant coefficients

Answer 8

Question 9

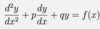
Give the standard form of a homogeneous second-order linear ODE with constant coefficients

Answer 9

Question 10

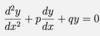
Describe how to get specific solutions to a second-order homogeneous linear ODE with constant coefficients

Answer 10

Substituting y = e^kx gives k² + pk + q = 0

Specific solutions are y₁ = e^k₁x and y₂ = e^k₂x

General solutions depend on the nature of k₁ and k₂

Question 11

Give the general solution to a second-order homogeneous linear ODE with constant coefficients if it has two real roots

Answer 11

Question 12

Give the general solution to a second-order homogeneous linear ODE with constant coefficients if it has complex roots, k_1,2 = α ± iβ

Answer 12

Question 13

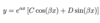
Give the general solution to a second-order homogeneous linear ODE with constant coefficients if it has degenerate roots

Answer 13

Question 14

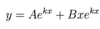
Give the standard form of an inhomogeneous second-order linear ODE with constant coefficients

Answer 14

Question 15

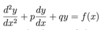
Describe how to solve an inhomogeneous second-order linear ODE with constant coefficients

Answer 15

First set f(x) = 0 and find the ‘complementary function y_CF(x)’ of the homogeneous ODE.

Find a particular integral y_PI(x), then y(x) = y_CF(x) + y_PI(x)