Number Properties on the GMAT

Question 1

Rational Numbers

Answer 1

All of the numbers that can be expressed as the ratio of two integers (all integers and fractions).

Question 2

Irrational Numbers

Answer 2

All real numbers that are not rational, both positive and negative (e.g., π, -√3)

Question 3

Properties of Integers

(Added, Subtracted, Multiplied, and Divided)

Answer 3

When an integer is added to, subtracted from, or multiplied by another integer, the result is an integer. An integer divided by an integer may or may not result in an integer.

Question 4

Rules for Evens and Odds

Odds x Odds =

Even x Even =

Odd x Even =

Answer 4

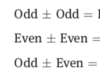
Odd x Odd = Odd

Even x Even = Even

Odd x Even = Even

Question 5

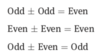
Exponent Rules for Odds and Evens

Odd^{any positive integer}

Even^{any positive integer}

Answer 5

Odd^{any positive integer} = Odd

Even^{any positive integer} = Even

Question 6

Properties of Numbers between -1 and 1

(Getting Reciprocal of a Fraction)

Answer 6

The reciprocal of a number between 0 and 1 is greater than the number itself.

(You can also easily get the reciprocal of a fraction by switching the numerator and denominator. The result will be the same. For example, the reciprocal of 2/3 is 3/2.)

The reciprocal of a number between -1 and 0 is less than the number itself.

Multiplying any positive number by a fraction between 0 and 1 gives a product smaller than the original number.

Multiplying any negative number by a fraction between 0 and 1 gives a product greater than the original number.

Question 7

Undefined

Answer 7

Division by zero is undefined. When given an algebraic expression, be sure that the denominator is not zero. The fraction 0/0 is likewise undefined.

Question 8

When multiplying or dividing numbers with the same sign, the result is …

When multiplying or dividing two numbers with different signs, the result is …

Answer 8

When multiplying or dividing numbers with the same sign, the result is always positive. When multiplying or dividing two numbers with different signs, the result is always negative.

Question 9

When Picking Numbers keep these things in mind

Answer 9

• Every number is a both a factor and a multiple of itself
• 1 is a factor of every number
• 0 is a multiple of every number

Question 10

Prime Number

Answer 10

• Integer greater than 1 that has only two positive factors, 1 and itself.
• Number 1 is not considered a prime
• Number 2 is only Even prime number

Question 11

Prime Factorization

Answer 11

Prime factorization of a number is the expression of the number as the product of its prime factors. No matter how you factor a number, its prime factors will always be the same.

The easiest way to determine a number’s prime factorization is to figure out a pair of factors of the number and then determine their factors, continuing the process until you’re lef with only prime numbers.

Question 12

When is a number divisble by 2

Answer 12

A number is divisible by 2 if its units digit is even.

138 is divisible by 2 because 8 is even.

177 is not divisible by 2 because 7 is not even.

Question 13

When is a number divisible by 3

Answer 13

A number is divisible by 3 if the sum of its digits is divisible by 3.

4,317 is divisible by 3 because 4 + 3 + 1 + 7 = 15 and 15 is divisible by 3.

32,872 is not divisible by 3 because 3 + 2 + 8 + 7 + 2 = 22 and 22 is not divisible by 3.

Question 14

When is a number divisble by 4

Answer 14

A number is divisible by 4 if its last two digits compose a two-digit number that is itself divisible by 4.

1,732 is divisible by 4 because 32 is divisible by 4.

1,746 is not divisible by 4 because 46 is not divisible by 4.

Question 15

When is a number divisible by 5

Answer 15

A number is divisible by 5 if its units digit is either a 5 or a 0.

26,985 is divisible by 5.

55,783 is not divisible by 5.

Question 16

When is a number divisible by 7

Answer 16

A number is divisible by 7 if the difference between its units digit multiplied by 2 and the rest of the number is a multiple of 7.

147 is divisible by 7 because 14 − 7(2) = 0, which is divisible by 7.
682 is not divisible by 7 because 68 − 2(2) = 64, which is not divisible by 7.

Question 17

When is a number divisible by 8

Answer 17

A number is divisible by 8 if its last three digits compose a three-digit number that is itself divisible by 8.

76,848 is divisible by 8 because 848 is divisible by 8.

65,102 is not divisible by 8 because 102 is not divisible by 8.

Question 18

When is a number divisible by 9

Answer 18

A number is divisible by 9 if the sum of its digits is divisible by 9.

16,956 is divisible by 9 because 1 + 6 + 9 + 5 + 6 = 27, and 27 is divisible by 9.

4,317 is not divisible by 9 because 4 + 3 + 1 + 7 = 15, and 15 is not divisible by 9.

Question 19

When is a number divisble by 11

Answer 19

A number is divisible by 11 if the difference between the sum of its odd-placed digits and the sum of its even-placed digits is divisible by 11.

5,181 is divisible by 11 because (5 + 8) − (1 + 1) = 11, which is divisible by 11.

5,577 is a multiple of 11 because (5 + 7) − (5 + 7) = 0, which is divisible by 11.

827 is not divisible by 11 because (8 + 7) − 2 = 13, which is not divisible by 11.

Question 20

Combining rules of factorizations to figure our divisibility of other numbers

Answer 20

You can combine these rules above with factorization to figure out whether a number is divisible

by other numbers.
To be divisible by 6, a number must pass the divisibility tests for both 2 and 3, since 6 = 2 × 3.

534 is divisible by 6 because 4 is divisible by 2 and 5 + 3 + 4 = 12, which is divisible by 3. To be divisible by 44, a number must pass the divisibility tests for both 4 and 11, since

44 = 4 × 11.
1,848 is divisible by 44 because 48 is divisible by 4 and (1 + 4) − (8 + 8) = −11, which is

divisible by 11.

Note that combining rules to test divisibility only works when the separate numbers you are testing do not have any factors in common (as is the case with 2 and 3 and with 4 and 11 above).

Question 21

Tricks for Sequences

Answer 21

Sequences can look complicated, and their descriptions can be confusingly worded. Paraphrase, simplify, and stay attuned to the patterns.