Arithmetic on the GMAT

Question 1

Division Methods - 1 - When dividing a decimal by a decimla†

Answer 1

-When dividing a decimal by another decimal, multiply each by a power of 10 such that the divisor becomes an integer; that is , move the decimal point of each the same number of places. (Doesn’t change the value of the quotient.) Then carry out the division as you would with integersm placing the decimal point in the quotient directly above the decimal point in the dividend. Example: 0.675 / 0.25 = Move the decimal point over two places t the right to make 0.25 an integer.

Question 2

Equivalent Fractions

(Radicals in the Denominator)

Answer 2

When you multiply the numerator and denominator by the same number (any number other than zero), the fraction is unchanged. You simply get an equivalent fraction.

Question 3

Dividing Complex Fractions - A complex fraction is a fraction that contains one or more fractions in its numerator or denominator. There are two methods for simplifying complex fractions. (Method 1 - Distributive)

Answer 3

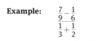
Method I: Use the distributive law. Find the least common multiple of all the denominators and multiply all the terms in the top and bottom of the complex fraction by the LCM. This will eliminate all the denominators, greatly simplifying the calculation.

Question 4

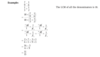
Dividing Complex Fractions - A complex fraction is a fraction that contains one or more fractions in its numerator or denominator. There are two methods for simplifying complex fractions. (Method 2 - Treat Numer/Denom seperately)

Answer 4

Treat the numerator and denominator separately. Combine the terms in each to get a single fraction on top and a single fraction on bottom. You are left with the division of two fractions, which you perform by multiplying the top fraction by the reciprocal of the bottom one. This method is preferable when it is difficult to get an LCM for all of the denominators.

Question 5

Division Methods - 2 - Turn into fraction

Answer 5

Turn the division problem into a fraction. It is best when the numbers have common factors. Move the decimal point in the numerator and the denominator an equivalent number of places to make both numbers integers. Then, cancel common factors.

Question 6

Fraction Pop Quiz 1

Answer 6

Question 7

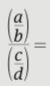
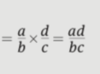
Common fractional to-deciaml equivalencies:

1/6

5/6

1/8

3/8

5/8

7/8

Answer 7

1/6 .1666

5/6 .8333

1/8 .125125

3/8 .375375

5/8 .625625

7/8 .875875

Question 8

Cmommon fraction-to-decimal equivalencies

1/9

2/9

4/9

5/9

1/12

1/16

1/32

Answer 8

1/9 0.111

2/9 0.222

4/9 0.444

5/9 0.555

1/12 0.08333…

1/16 0.0625

1/32 0.03125

Question 9

Exponents Pop Quiz 1

a^b x a^c

a^b / a^c

(a^b)^c

(a^b)(c^b)

a^-b

Answer 9

a^b x a^c = a^(b+c)

a^b / a^c = a^(b-c)

(a^b)^c = a^{b x c}

(a^b)(c^b) = (a x c)^b

a^-b = 1 / a^b

Question 10

Raising a positive fraction less than 1 to a positive exponent greater than 1 results in?

(higher/smaller result)?

Answer 10

Raising a positive fraction less than 1 to a positive exponent greater than 1 results in a smaller value. The higher the exponent, the smaller the result.

Question 11

When a negative number is raised to an even/odd exponent, the result is?

(Positive/Negative)?

Answer 11

When a negative number is raised to an even exponent, the result is positive. When a negative number is raised to an odd exponent, the result is negative.

Question 12

Answer 12

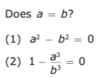
Statement (1) says that a² − b² = 0, which is the same as saying a² = b², then either a = b or a = −b. You can test a few cases by picking numbers. If a = 5 and b = 5, then a² = b², so Statement (1) is true and a = b. The answer to the question is yes.

If a = 5 and b = −5, then a² = b² because 5² = (−5)² = 25, so Statement (1) is true and a is not equal to b. The answer to the question is no. Because more than one answer to the question is possible, Statement (1) is insufficient.

Statement (2) tells you that 1−a³=0, which can be simplified as 1−(a³)/(b³) or a³ = b³. In the equation a3 = b3, both a and b are raised to the same odd exponent.

When raised to an odd power, positive numbers yield positive results and negative numbers yield negative results. So, if a3 = b3 you can now conclude that a = b. The answer to the question is always yes, and Statement (2) is sufficient. The correct answer is (B).

Question 13

When multiplying a number by a power of 10…

Answer 13

When multiplying a number by a power of 10, the exponent just represents the number of places to move the decimal.

Question 14

Answer 14

Question 15

Answer 15

Question 16

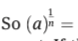
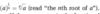
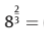
Multiplying or divide one radical by another

6√3 x 2√5 =

12√15 / 2√5 =

Answer 16

Multiply or Divide the numbers outside the radical signs, then the numbers inside the radical sign.

6√3 x 2√5 = (6*2) x (√3 x √5) = 12√15

12√15 / 2√5 = (12/2) x (√15/√5) = 6√3

Question 17

√ab =

√(a/b) =

√(a+b) >=<

√(a-b) >=<

(√a)² =

√(a²) =

a^½ =

a^{(b/c) =}

Answer 17

√ab = √a x √b

√(a/b) =(√a)/(√b)

√(a+b) >=< √a + √b

√(a-b) >=< √a - √b

(√a)² = a

√(a²) = |a|

a^½ = √a

a^{(b/c) =} (^c√a)^b

Question 18

(√13⁴) =

(³√7⁶) =

Answer 18

(√13⁴) = 13²

(³√7⁶) = 7²

If an exponent is under a square root sign, just divide the exponent by 2. If an exponent is under a cube root sign, divide it by 3.

Question 19

(√0.0009) =

(³√0.000125) =

Answer 19

(√0.0009) = 0.03

(³√0.000125) = 0.05

If a decimal is under a square root sign, take the square root of the number and divide the number of decimals places by 2. Likewise, if a deicmal isunder a cube root , take the cube root of the number and divide the number of decimal places by 3.

Question 20

Dealing with Absolute Value

Answer 20

1. Interpret absolute value as the expression’s distance from zero on the number line.
2. Draw a number line.
3. Write two equations for every equation with an absolute value; one or the other of these new equations must be true.

When there is an absolute value sign, there is a high likelihood of a trap answer for those who assume the quantity inside can only be positive.

Question 21

Solving Inequalities with multiplication or division of a negative number

Answer 21

If the Ineqaulity is multiplied or divide by a negative number, the direction of the inequality is reversed.

Question 22

Ineqaulities Solve for:

a specific value?

or

a range of values

Answer 22

Range of Values

Question 23

When Equal Powers have the same base

(where the same base is not -1,0,1):

4^2x+2 = (4²)^3x-1

Answer 23

The exponents must be equal

4^2x+2 = (4²)^3x-1

2x + 2 = 2 x (3x-1)

4 = 4x

x = 1