National 5 Projectiles & Space

Question 1

What is a projectile?

Answer 1

A projectile is an object which has two components of motion:

1. a horizontal uniform velocity, and
2. a vertical uniform acceleration downwards under gravity.

This causes the projectile to follow a parabolic trajectory (path).

Question 2

Explain the curved path of a projectile.

Answer 2

A projectile has constant horizontal velocity and constant vertical acceleration due to gravity.

Question 3

For projectile motion, what is the only equation you should use for the horizontal part of the motion?

Answer 3

For the horizontal part of the motion, the only equation which should be used is

Question 4

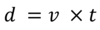
For projectile motion, what is the only equation you should use for the vertical part of the motion?

Answer 4

For the vertical part of the motion, the only equation which should be used is

Question 5

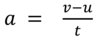
Explain the orbit of a satellite in terms of projectile motion.

Answer 5

A satellite is a projectile: it is travelling horizontally with a constant velocity, but also accelerating vertically downwards so that the curve of its path (trajectory) matches the curve of the planet it is orbiting.

Question 6

What is the relationship between the altitude of a satellite (height above the Earth) and its period (time taken to complete one orbit of the Earth)?

Answer 6

The higher the altitude, the longer the period of the satellite.

Question 7

Describe some of the benefits of satellites.

Answer 7

Satellites have helped to develop:

• The accuracy of weather forecasting
• Worldwide continuous telecommunication
• Analysis of our environment
• National security
• Sat-Nav/GPS systems
• Our understanding of the universe through space telescopes
• Our understanding of science through experiments performed in space (e.g. on the ISS)

Question 8

What is meant by a geostationary orbit?

Answer 8

A geostationary orbit is an orbit in which a satellite would appear stationary when viewed from the Earth.

Question 9

What are the properties of a geostationary orbit?

Answer 9

• The orbital period is 24 hours.
• The altitude is 36 000 km
• The orbit is above the equator

Question 10

What are the advantages of a geostationary orbit?

Answer 10

Since satellites in geostationary orbit do not appear to move from Earth, satellite dishes can be stationary and don’t need to ‘track’ the position of the satellite.

It also means that the satellite will never go out of view and continuous communication is available.

Question 11

Describe some of the challenges associated with space exploration and possible solutions to these.

Answer 11

• Travelling the large distances in space: This could be addressed using ion propulsion to produce a small unbalanced force over a large period of time.
• Travelling the large distances in space: Another solution that has already been used is a ‘slingshot’ effect by passing close to a fast moving asteroid, moon or planet.
• Manoeuvring a spacecraft in a zero friction environment is very difficult. Computers can be used to aid this.
• Maintaining sufficient energy to operate life support systems in a spacecraft for long periods of time. A possible solution is using solar cells or nuclear reactors.

Question 12

Describe some of the risks of space exploration.

Answer 12

• The fuel load on take-off can lead to fire and explosions
• Astronauts can be exposed to a high level of radiation, without the Earth’s atmosphere to absorb some of the cosmic rays
• Space is a vacuum, and so there is a large difference in pressure between the inside of a spacecraft (or spacesuit) and outside
• Re-entry to a planet’s atmosphere creates a large amount of heat due to air resistance. Thermal protection systems must be used to ensure the spacecraft is protected on re-entry.
• The angle of re-entry must be precisely calculated so the spacecraft doesn’t ‘bounce off’ the atmosphere or enter too fast.

Question 13

Define what a light year is.

Answer 13

A light year is the distance travelled by light in one year.

Question 14

Why are distances in space measured in light-years?

Answer 14

Distances in space are vast. They are too big to be easily understood using metres. A light-year is large enough to be suitable for describing the distance between objects in space.

Question 15

Describe how to calculate one light-year in metres.

Answer 15

Use the formula d = v x t :

• v = 3 x 10⁸ ms^-1 (speed of light)
• t = 1 year (convert into s: 365.25 x 24 x 60 x 60)
• Calculate d

Question 16

Describe what is meant by the Big Bang.

Answer 16

The Big Bang marks the start of the universe, when everything was in an unimaginably small volume (almost a point) and rapidly expanded.

Question 17

State the approximate age of the universe.

Answer 17

Our current estimate of the age of the universe is 13.8 billion years.

Question 18

What is meant by the ‘observable universe’?

Answer 18

The furthest point in space that we can see is the distance light must have travelled for the whole age of the universe.

Everything within this distance is called the ‘observable universe’.

Question 19

What is a planet?

Answer 19

A planet is a large object in orbit around a star. (large enough to have cleared its own path of debris)

Question 20

What is a dwarf planet?

Answer 20

A dwarf planet is an object which orbits the Sun but whose orbit is not uniform enough to be classed as a planet due its small mass.

Question 21

What is a moon?

Answer 21

A moon is a natural satellite of a planet.

Question 22

What is the Sun?

Answer 22

The Sun is the star at the centre of our solar system.

Question 23

What is an asteroid?

Answer 23

An asteroid is a small rocky body orbiting the Sun.

Question 24

What is a solar system?

Answer 24

A solar system is a collection of objects orbiting a star.

Question 25

What is a star?

Answer 25

A star is a sphere of gas (plasma) undergoing nuclear fusion and emitting heat and light.

Question 26

What is an exo-planet?

Answer 26

An exo-planet is a planet outwith our solar system i.e orbiting a star other than the Sun.

Question 27

What is required for a planet to be able to sustain life?

Answer 27

To sustain life as we know it, a planet must be within the right temperature range - it must be capable of having liquid water and an oxygen-rich atmosphere.

Question 28

What is a galaxy?

Answer 28

A galaxy is a group of stars, gases and dust held together by gravity.

Question 29

What is the universe?

Answer 29

The universe is all existing matter and space.

Question 30

What are the different types of wave detected by space telescopes?

Answer 30

As well as visible light, telescopes detect radio waves, infrared (IR), ultraviolet (UV), X-rays and Gamma rays to obtain information about astronomical objects.

Question 31

What name is given to this pattern, produced when a source of white light is viewed through a spectroscope?

Answer 31

When white light is viewed through a spectroscope, a continuous spectrum is produced.

Question 32

What name is given to this pattern, produced when hot elements in gas form are viewed through a spectroscope?

Answer 32

A line spectrum.

Question 33

In space physics, how do scientists use line spectra?

Answer 33

Each element has a unique line spectrum so scientists use these to identify the different elements present in stars and galaxies.