National 5 Mechanics Flashcards
Factual Recall
- Define what is meant by vector and scalar quantities.
A vector quantity has a magnitude and direction. A scalar quantity only has a magnitude.
- State which of the following list are vector and which are scalar quantities:
force, speed, velocity, distance, displacement, acceleration, mass, time and
energy.
Vector
Force, velocity, displacement, acceleration
Scalar
Speed, distance, mass, time and energy
- State the difference between distance and displacement.
Distance is a measure of how far an object has travelled.
Displacement is the length and direction travelled in a straight line from the starting point to the finishing point.
- Describe how to work out displacement and/or distance using scale diagram or calculation.
For total distance, simply add up the individual distances.
For resultant displacement, sketch a diagram then use Pythagoras (a2 = b2 + c2) to find the hypotenuse, which will be the resultant displacement, and use Trig (tan(x)=Opp/Adj) to find the angle.
- Example of how to work out displacement and/or distance using scale diagram or calculation:
A walker travels 12km South then 5km West. Calculate:
a) the distance travelled
b) the resultant displacement
(See Image)

a) d = 12 + 5 = 17 km
b) a2 = b2 + c2
a2 = 52 + 122 = 25 + 144 = 169
a = sqrt(169) = 13 km
tan(x) = Opp/Adj = 5/12
x = tan-1(5/12) = 27º
Bearing is clockwise from North i.e. 180 + 27 = 207º
Resultant Displacement is 13 km bearing 207º
- State the difference between speed and velocity.
Speed is the distance travelled every second and is a scalar.
Velocity is the displacement travelled every second in a certain direction and is a vector.
- Describe an experiment to measure an average speed
You would measure the total distance travelled (d) with a measuring tape and the time taken to cover this distance (t) using a stopwatch. You calculate the average speed (v) by dividing this distance (d) by this time (t).
d = vt
(Define symbols and units)
d - distance (m) or (km)
v - speed (ms-1) or (kmh-1)
t - time (s) or (h)
- Example
You run at a steady speed of 6 ms-1 for 5 minutes. How far did you go?
v = 6 ms<sup>-1</sup> t = 5 min = 5 x 60 = 300 s d = ?
d = vt
= 6x300
d = 1,800 m
d = vt
(Define symbols and units)
d - total distance (m) or (km)
v - average speed (ms-1) or (kmh-1)
t - total time (s) or (h)
- Example
At the 2008 Beijing Olympics, Usain Bolt ran 100m in 9.69 seconds. Calculate his average speed.
d = 100 m t = 9.69 s v = ?
d = v t
100 = v x 9.69
v x 9.69 = 100
v = 100/9.69
v = 10.32 ms-1
s = vt
(Define symbols and units)
s - displacement (m) or (km)
v - velocity (ms-1) or (kmh-1)
t - time (s) or (h)
- Example
James sends a bowling ball off at 8.81 ms-1 North. The first pin is 18.29 m North.
How long does it take for the bowl to hit the pin?
Direction is consistent. Time is a scalar so no direction required.
v = 8.81 ms<sup>-1</sup> s = 18.29 m t = ?
d = vt 18.29 = 8.81xt 8.81xt = 18.29 t = 18.29/8.81 t = 2.08 s
s = vt
(Define symbols and units)
s - resultant displacement (m) or (km)
v - average velocity (ms-1) or (kmh-1)
t - total time (s) or (h)
- Example of how to work out average speed and average velocity using scale diagram or calculation:
A walker travels 12km South then 5km West in 4 hours. Calculate:
a) the distance travelled
b) the resultant displacement
c) the average speed
d) the average velocity
(See Image)

a) d = 12 + 5 = 17 km
b) a2 = b2 + c2
a2 = 52 + 122 = 25 + 144 = 169
a = sqrt(169) = 13 km
tan(x) = Opp/Adj = 5/12
x = tan-1(5/12) = 27º
Bearing is clockwise from North i.e. 180 + 27 = 207º
Resultant Displacement is 13 km bearing 207º
c) d = 17 km; t = 4 h; v = ?
d = vt
17 = v x 4
v x 4 = 17
v = 17/4 = 4.25 kmh-1
d) s = 13 km (207º); t = 4 h; v = ?
s = vt
13 = v x 4
v x 4 = 13
v = 13/4 = 3.25 kmh-1 (207º)
- Describe an experiment to measure instantaneous speed.
You would use a light gate and a mask. Measure the length of the mask (d) with a ruler and the time taken for the mask to go through the light gate (t) using an attached timer. You calculate the instantaneous speed (v) by dividing this distance (d) by this time (t).

- Identify situations where average velocity and instantaneous velocity are different.
Average and instantaneous velocity are different during a sprint race where the runners start from rest then accelerate.
- Describe how to calculate the resultant of two vector quantities at right angles.
Use Pythagoras and Trig:
Draw a diagram, following the head to tail rule. Use Pythagoras (a2 = b2 + c2) to find the hypotenuse, which will be the resultant and use tan(θ) = Opp/Adj to find the angle.
- Example calculation of the resultant of two vector quantities at right angles.
See Image

a2 = b2 + c2
a2 = 302 + 402 = 900 + 1600 = 2500
a = √2500 = 50 N
tan(θ) = Opp/Adj = 40/30
θ = tan-1(40/30) = 53º
Bearing is clockwise from North i.e. 90-53=37º
Resultant Force is 50 N bearing 037º
- Describe how to calculate the resultant of two vector quantities in one dimension.
Sketch a diagram.
Add all the vectors in one direction and subtract all the vectors in the opposite direction.
- Example calculation of the resultant of two vector quantities in one dimension.
Two girls pull a car with a force of 100N each, while friction applies an opposing force of 80N. Calculate the resultant force.
FR = 100 + 100 - 80 = 120N
- Describe how to draw velocity-time graphs or speed-time graphs from data.
Label both axes with quantity and units.
Label the origin.
Draw straight lines for each section of the motion: diagonally upwards for acceleration, straight across for constant speed, diagonally downwards for decceleration.
- Example of velocity-time graphs or speed-time graphs from data.
A sprinter accelerates from rest to 12 ms-1 in 2 s, holds this speed steady for 6s, then deccelerates to 10 ms-1 as they cross the line.

- Describe the motion shown in this graph.

Constant Velocity
- Describe the motion shown in this graph.

Constant Acceleration
- Describe the motion shown in this graph.

Constant Decceleration
- Describe how to determine the displacement from a velocity-time graph.
Use s = area under graph
Split the area under the graph (i.e. from the line to the x-axis) into rectangles and triangles.
Calculate the area of each using bh and ½bh.
- Example: calculate the displacement from this velocity-time graph

s = Area Under Graph
(See Image for identifying triangles and rectangles)
s = ½bh + bh + ½bh + bh
s = ½x2x12 + 6x12 + ½x2x2 + 2x10
s = 106m

- Define acceleration.
Acceleration is the change in velocity per second.
- State what is meant by an acceleration of 5 ms-2.
The velocity increases by 5 ms-1 every second.
- a = (v-u)/t
(Define symbols and units)
a - acceleration or decceleration (ms-2)
v - final velocity (ms-1)
u - initial velocity (ms-1)
t - time (s)
- Example
A dancer accelerates from rest to 4 ms-1 in a time of 0.5 s.
Calculate their acceleration.
u = 0 ms<sup>-1</sup> (Remember information can be given in words) v = 4 ms<sup>-1</sup> t = 0.5 s a = ?
a = (v-u)/t a = (4-0)/0.5 a = 8.0 ms<sup>-2</sup>
- Example
A car brakes to a halt from 30 ms-1 in a time of 4s.
Calculate their decceleration.
Decceleration is calculated using the acceleration formula, but should give a negative answer.
v = 0 ms<sup>-1</sup> (in words) u = 30 ms<sup>-1</sup> t = 4 s a = ?
a = (v-u)/t a = (0-30)/4 a = -7.5 ms<sup>-2</sup>
- Example
A tennis ball accelerates from rest with an acceleration of 40 ms-2 for 0.05 s.
Calculate its final speed.
u = 0 ms<sup>-1</sup> (Remember information can be given in words) a = 40 ms<sup>-2</sup> t = 0.05 s v = ?
a = (v-u)/t
40 = (v-0)/0.05
40 x 0.05 = v
v = 2 ms-1
- Example
A rocket has an acceleration of 90 ms-2.
It needs to reach a speed of 11,000 ms-1 to escape the Earth.
How long from launch will this take?
a = 90 ms<sup>-2</sup> v = 11,000 ms<sup>-1</sup> u = 0 ms<sup>-1</sup> (in words - from launch) t = ?
a = (v-u)/t
90 = (11,000-0)/t
90 = 11,000/t
90 x t = 11,000
t = 11,000/90
t = 122 s
- Describe an experiment to measure acceleration.
Ensure that the mask cuts the light gates. Measure the length of the mask (d) using a ruler. Using the timer measure the times for the mask to cut the first light gate (t1), the second light gate (t2) and the time for the mask to travel between light gates (t). Calculate the initial velocity (u) using u=d/t1 and the final velocity (v) using v=d/t2. Calculate the acceleration (a) using a = (v-u)/t.

- Example of how to calculate acceleration from v-t graphs
Calculate the acceleration and decceleration in this motion.
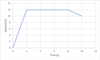
Accleration
u = 0 ms-1
v = 12 ms-1
t = 2 s
a = (v-u)/t
a = (12-0)/2
a = 6 ms-2
Deccleration
u = 12 ms-1
v = 10 ms-1
t = 10-8 = 2 s
a = (v-u)/t
a = (10-12)/2
a = -1 ms-2
- Describe the effects of friction.
Friction is a force which opposes the motion of an object, making moving objects slow down and keeping stationary objects still.
- Compare motion in situations of high and low friction:
Give an example of a useful decrease in friction.
Low friction is important in allowing objects to move faster e.g. putting wax on the bottom of skies.
- Compare motion in situations of high and low friction:
Give an example of a useful increase in friction.
High friction can be used to slow down moving objects e.g. bike brakes rubbing against the wheel.
- Explain what is meant by balanced forces.
Balanced forces are forces which are equal in size but in the opposite direction so that the resultant force is zero.
- Explain the term mass.
Mass is the amount of matter that makes up an object. It is a scalar quantity and is measured in kilograms (kg).
- Explain the term weight.
Weight is the gravitational force acting on an object. It is a vector quantity and is measured in newtons (N).
- Explain the term gravitational field strength.
Gravitational field strength is the weight per unit mass. On earth, g is 9.8 Nkg-1.
- W = mg
(Define symbols and units)
W - weight (N)
m - mass (kg)
g - gravitational field strength (Nkg-1)
- Example
An astronaut has a mass of 60 kg.
Calculate her weight on Mars, where g = 3.7 Nkg-1.
m = 60 kg g = 3.7 Nkg<sup>-1</sup> (You would usually get this from a Data Sheet) W = ?
W = mg W = 60 x 3.7 W = 222 N
- State Newton’s First Law.
An object will remain at rest or move at a constant speed in a straight line unless acted on by an unbalanced force.
- F = ma
(Define symbols and units)
F - Unbalanced or Resultant Force (N)
m - mass (kg)
a - acceleration (ms-2)
- Example
Calculate the unbalanced force on a rocket of mass 60,000 kg with an acceleration of 90 ms-2.
m = 60,000 kg a = 90 ms<sup>-2</sup> F = ?
F = ma F = 60,000 x 90 F = 5,400,000 N
- Example
Two girls pull a car of mass 1000 kg with a force of 100N each, while friction applies an opposing force of 80N. Calculate the acceleration.
Sketch a diagram when dealing with more than one force.
F<sub>UN</sub> = 100 + 100 - 80 = 120N m = 1000 kg a = ?
F = ma
120 = 1000 x a
1000 x a = 120
a = 120/1000
a = 0.12 ms-2
- Apply Newton’s Laws to explain or determine a body’s acceleration when more than one force is acting at right angles.
Example:
A toy boat’s engine applies a force of 40N North while river current applies a force of 30N East. The mass of the boat is 20 kg. Calculate it’s acceleration.
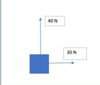
Redraw vector diagram nose to tail if required.
a2 = b2 + c2
a2 = 302 + 402 = 900 + 1600 = 2500
a = √2500 = 50 N
tan(x) = Opp/Adj = 30/40
x = tan-1(30/40) = 37º
Resultant Force is 50 N bearing 037º
F<sub>UN</sub> = ma 50 = 20 x a a = 50/20 = 2.5 ms<sup>-2</sup> bearing 037º

- Apply Newton’s 2nd Law to space travel, including rocket launch and landing.
Example:
At launch, a rocket of mass 2000 kg produces a thrust of 25,000 N. Calculate its acceleration.
Draw a sketch diagram, adding in all forces.
Since it moves vertically, we need to add in Weight.
Since it says “At launch” it’s not yet moving, so we can neglect air resistance.
W = mg = 2000 x 9.8 = 19,600 N
FUN = T - W = 25,000 - 19,600 = 5,400 N
F<sub>UN</sub> = ma 5400 = 2000 x a a = 5400/2000 = 2.7 ms<sup>-2</sup> upwards

- State Newton’s Third Law.
If an object A exerts a force on object B, then B exerts a force on A which is equal in size but in the opposite direction.
- Identify “Newton’s Third Law pairs” in situations involving several forces.
e.g. a book sitting on a table pushes down on the table, while the table pushes up on the book.
- Use Newton’s Third Law to explain motion resulting from a reaction force.
e.g. a rocket pushes gases out the back and the gases push the rocket forward.
- Use Newton’s laws to explain free-fall.
Free-fall describes the movement of any object under the influence of gravity/weight alone.
In this case F = W,
so ma = mg (by Newton’s 2nd Law)
and a = g (dividing both sides by m)
All objects on earth, no matter their mass, accelerate at 9.8 ms-2.
- Use Newton’s laws to explain terminal velocity.
When an object is first dropped, its weight provides an unbalanced force, causing it to accelerate downwards by Newton’s 2nd Law. The air resistance acting on it will increase as it speeds up. By Newton’s First Law it will reach a steady velocity, called its terminal velocity, when the upward force on the object (air resistance) balances the downward force on the object (weight).
- Explain the concept of work done.
The amount of energy changed/transferred by a Force.
- Ew = Fd
(Define symbols and units)
Ew - Work Done (J)
F - Applied Force (N)
d - distance (m)
- Example
Calculate the work done by an ant carryin a leaf with a force of 5 mN over a distance of 20 m.
F = 5 mN = 0.005 N d = 20 m E<sub>w</sub> = ?
E<sub>w</sub> = Fd E<sub>w</sub> = 0.005 x 20 E<sub>w</sub> = 0.1 J
- Ep = mgh
(Define symbols and units)
Ep - (Gravitational) Potential Energy (J)
m - mass (kg)
g - gravitational field strength (Nkg-1)
h - height (m)
- Example
Estimate the gravitational potential energy you gain when walking up 3 flight of stairs to the Physics department.
m = 50 kg (estimate) h = 10 m (estimate) g = 9.8 Nkg<sup>-1</sup> (Data Sheet) E<sub>p</sub> = ?
E<sub>p</sub> = mgh E<sub>p</sub> = 50 x 9.8 x 10 E<sub>p</sub> = 4,900 J
- Define gravitational potential energy.
The energy stored by an object as a result of its vertical position (height) above the surface of the Earth.
- Ek = ½mv2
(Define symbols and units)
Ek - Kinetic Energy (J)
m - mass (kg)
v - velocity (ms-1)
- Example
Calculate the kinetic energy of a horse and rider travelling at 15 ms-1. Their combined mass is 600 kg.
m = 600 kg v = 15 ms<sup>-1</sup> E<sub>k</sub> = ?
E<sub>k</sub> = ½mv<sup>2</sup> E<sub>k</sub> = ½ x 600 x 15<sup>2</sup> E<sub>k</sub> = 67,500 J
- Example
Calculate the speed of a bird of mass 2 kg and a kinetic energy of 25 J.
m = 2 kg v = ? E<sub>k</sub> = 25 J
E<sub>k</sub> = ½mv<sup>2</sup> 25 = ½ x 2 x v<sup>2</sup> 25 = 1 x v<sup>2</sup> v<sup>2</sup> = 25 v = √25 = 5 ms<sup>-1</sup>
- Define kinetic energy.
The energy possessed by an object because of its movement.
- Define power.
The work done/energy transferred per second.
- P = E/t
(Define symbols and units)
P - Power (W)
E - Energy (J)
t - time (s)
- Example
Running a mile and walking a mile use roughly the same energy e.g. 135,000 J for an adult male.
Calculate the power required to
a) run a mile in 5 min
b) walk a mile in 20 min
a) E = 135,000 J
t = 5 min = 5 x 60 = 300 s
P = ?
P = E/t P = 135,000/300 P = 450 W
b) E = 135,000 J
t = 20 min = 20 x 60 = 1200 s
P = ?
P = E/t P = 135,000/1200 P = 113 W
- State the principle of conservation of energy.
Energy cannot be created or destroyed, but can change from one form to another.
- Carry out calculations involving conservation of energy.
Example:
A ball of mass 2.0 kg is dropped from a height of 3.0 m. Calculate it’s speed when it hits the ground.
Identify the main energy change: Gravitational Potential to Kinetic
Conservation of energy tells us that in the absence of energy being lost these two values must be equal to each other.
Ep = Ek
mgh = ½mv2
(Note that we could cancel m from both sides)
2 x 9.8 x 3 = 12 x 2 x v2
58.8 = v2
v = √58.8 = 7.67 ms-1
- Identify and explain the “loss” of energy where energy is transferred.
When energy is transferred, not all will necessarily be transferred into a useful form and is considered lost e.g. a light bulb converts electrical energy into light (useful) and heat (not useful) which is lost to the surroundings.


