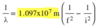Moles / Light Flashcards
1
Q
1 mole
A
- 6.022 x 1023 atoms
- As many particles as there are in 12.0 g of 12C
- Avagadro’s number
2
Q
Molar conversions
A

3
Q
A mole of a compound (covalent, ionic)
A
-
Covalent: Avogadro’s number of molecules
- 1 mole CO2 = 6.022 x 1023 CO2 molecules
- Ionic: Avogadro’s number of formula units
4
Q
How many moles of C, H, O in C6H12O2?
A
- C) 6 moles
- H) 12 moles
- O) 6 moles
5
Q
How to find molar mass
A
- Add for each element:
- Number of moles in the element * atomic mass (from periodic table, g/mole)
6
Q
Electromagnetic radiation
A
- Generated by moving electrons
- Can transport energy without a medium (unlike sound which requires matter to move through)
- Displays wave properties
- Diffraction
- Interference
7
Q
Electromagnetic spectrum
A

8
Q
Features of waves
A
-
Wavelength: the distance between two identical points on two asjacent waves
- Symbol: lambda λ
- Unit: m, nm
- 109 nm in m

9
Q
Frequency
A
- The amount of crests that pass a point in one second
- Symbol: f, nu, ν
- Unit: s-1, Hz
10
Q
Relationship between wavelength and frequency
A
- All EM waves travel at speed of light
- c = 3.0 x 108 m/s
- c = λv
- Long wavelength = low frequency
- Short wavelength = high frequency

11
Q
Max Planck
A
- Solids emit radiation as heated
- Study relationships between wavelength and intensity of radiation emitted and temperature
- Energy is quantizes
- Lower frequency = intense light
12
Q
Quantization of energy
A
- Energy is released or absorbed in quanta
- Energy radiation is directly proportional to frequency (specific allowable energies)
- Quantized - values are restricted to certain quantities
13
Q
Energy equation (Planck’s constant)
A
- E = hv
- h = Planck’s constant = 6.626 x 10-34 J S
- v = frequency
14
Q
Wavelength vs energy vs frequency (red vs violet)
A
- RED: Large wavelength = low frequency = low energy
- VIOLET: Small wavelength = high frequency = high energy
15
Q
Photoelectric effect
A
- When light is shone on a metal, electrons are ejected from the metal
- The ejected electrons have a ceratin amount of kinetic energy
16
Q
Classical physics prediction
A
- Higher amplitude (brighter) = more energy
- Bright red = eject electrons, dim red = no electrons
- Bright blue = eject electrons, dim blue = no electrons
- Brighter light = higher energy of electrons popped off
17
Q
Blue vs red light actually observed
A
- Bright red = no electrons, dim red = no electrons
- Bright blue = eject electrons, dim blue = eject electrons (but fewer)
- Suggests that the ability of light to eject electrons depends on its frequency, not brightness
- Planck - energy and frequency directly related
- Einstein uses this to explain the photoelectric effect
18
Q
Einstein explains photoelectric effect
A
- Light as particles, each with its own quantum (specific amount) of energy, depending on its frequency
- Particles called photons
- Only those photons with the minimum amount of energy needed to eject electrons from metal will do so
19
Q
Photon
A
- A particle of electromagnetic radiation having zero mass and carrying a quantum of energy
- Light has a dual nature
20
Q
Classical view of atom
A
- An electron traveled about the nucleus in an orbit
- Any orbit should be possible for any electron
- Did not know why the electrons did not fall into the nucleus
21
Q
Neils Bhor
A
- Built a simple model of an atom
- Based on an understanding of the sharp line emission spectrum of excited atoms
22
Q
Line emission spectra
A
- When atoms or molecules absorb energy, that energy is often released as light energy (fireworks, etc)
- When that light is passed through a prism. a pattern is seen that is unique to that type of atom or molecule — pattern called an emission spectrum
- Non-continuous
- Can be used to identify the material
- Flame tests
23
Q
Line emission spectra of excited atoms
A
- Excited atoms emit light of only certain wavelengths
- The wavelengths of emitted light depend on the element
24
Q
Ground state
A
Electron in lowest energy level possible
25
Atomic spectra and Bhor
* e- can only exist in certain **discrete orbits** of specific energy (quantized energy states)
* e- have a **specific** amount of energy that is equal to the PE of their location
* PE of e- is determined by its distance from the nucleus
* Closer to nucleus = lower PE
* Each type of photon has an energy equal to the energy lost by specific jumps in energy levels
* Nobel prize 1922
* **Problem**: only works for hydrogen --\> quantum/wave mechanics
26
Balmer series
* The series of visible lines in the hydrogen atom spectrum

27
L de Broglie (+ equations)
* Proposed (1924) that all moving objects have wave properties
* For light: E = mc2
* E = hν = hc / λ
* mc = h / λ
* For particles: c = velocity
* (mass)(velocity) = h / λ
* mv = h / λ
* λ = h / mv
28
Quantum / wave mechanics (+ equation)
* Using deBroglie's equation **λ = h/mv** can calulcate the wavelength for moving objects
* λ = wavlength (meters)
* v = velocity (m/sec)
* m = mass (kg)
* h = Planck's constant
29
Uncertainty principle
* Problem of defining nature of electrons in atoms
* Solved by W. **Heisenberg**
* Cannot simultaneously define the **position** and **momentum** (m\*v) of an electron
* We define e- energy exactly but accept limitation that we do not know exact position
* m = kg
* v = m/s

30
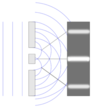
Double slit experiment
* Demonstration that light and matter can display characteristics of both classically defined waves and particles
* Electrons act like waves and particles
* Interference pattern
31
E Schrodinger
* Applied idea of e- behaving as a wave to the problem of electrons in atoms
* Developed the **wave equation**
* Solution gives set of math expressions called **wave functions**
* Each wave function describes an allowed energy state of an e- which corresponds to an **_orbital_** - the region of space within which an electron is found
* Area of probability, not exact location
32
Orbital
* For an electron with a given energy, can describe a region in the atom of high probability of finding it
* Many of the properties of atoms are related to the energies of the electrons
33
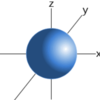
s orbital
* 1 direction spherical
34
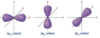
p orbital
* 3 directions
* Three p orbitals lie 90 degrees apart in space
35
d orbital
* 5 directions
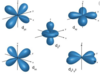
36
f orbital
* 7 directions

37
g orbital
* 9 directions
* Hypothetical

38
Principal quantum number
* Symbol: n
* The main energy level occupied by the electron
* Values of n are positive integers and the value of n=1 has the lowest energy
39
Sublevels and relative energy
* 4 sublevels for the elements discovered to date
* Sublevel indicates the shape of the orbital
* First energy level, n = 1 has 1 sublevel
* Fourth energy level, n = 4 has 4 sublevels
* Levels split because negative e- next to each other
* Sublevels broken up into orbitals

40
The Aufbau Rule
* The **lowest** energy levels are filled first
41
The Pauli Exclusion Principle
* Orbitals can have **max of 2 electrons**
* e- in same orbital must have **opposite** spins
42
Hund's Rule
* When orbitals of identical energy (same shape) are available, e- enter those orbitals singly before any spin pairing takes place
43
Energy emitted by e- energy level change
E in J
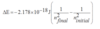
44
Wavelength emitted by e- energy level change