Mechanics/ biomechanics - unit 1 deck 1 Flashcards
Describe what is meant by saying ‘the choice of scale for a unit’
This is referring to the size range of any particular type of unit.
e.g. the main metric unit of distance is the metre but you have a choice of also using micrometres, millimetres, centimetres or kilometres. These different choices is a choice of scale
What is the single system of units referred to as ?
System Internationale d’Unites - known as SI units
This is just a system which came up with the standard units you should use
What are the 3 main base units in Systeme Internationale (SI) relevant to this module ?
- The metre (m) - the standard unit of length
- The second (s) - the standard unit of time
- The kilogram (kg) - the standard unit of mass
What is the 4th base SI unit which we should know about relevant to the biomechanics module?
kelvin (K) - the standard SI unit of temperature.
What is the relevant supplementary unit in the SI system which is relevant to this module ?
The radian (rad) - the standard unit of angle
What are the units other than the base SI units and supplementary SI units referred to as and how are they formed ?
The are referred to as derived units and are formed by combining base units
e.g. the newton (N) is equivalent to kilogram metres per second squared (kg m s-2 )
What do each of the following scale factors that you should remember stand for:
- mega (M) -
- kilo (K) -
- centi (c) -
- milli (m) -
- micro (µ) -
- mega (M) - x106
- kilo (K) - x103
- centi (c) - x10-2
- milli (m) - x10-3
- micro (µ) - x10-6
What are the 3 rules you need to remember to follow when using units ? i.e. m, cm, km, s, etc etc
- Write prefixes without a space, e.g. cm (there is no space between the c and the m)
- Leave a space between symbols for units e.g. m s-1 (metres per second) not ms-1 as this reads as ‘‘per millisecond’’
- Never pluralise units, e.g. 10ms means 10 milliseconds not 10 metres
What are the 4 basic physical quantities and state their SI units that we should know about in mechanics and biomechanics
- Time - SI unit is seconds (s)
- Distance - SI unit is meters (m)
- Angle - SI unit is radian (rad), note that the common unit of angle is the degree
- Temperature - SI unit is kelvin (K)
What are the common units of temperature used ?
Degrees Celsius, represented by the symbol °C
What is the Celsius scale based on ?
The melting and bioling point of water
- 0 degrees = melting point of water
- 100 degrees = bioling point of water
What does 0K represent and what is this the equivalent of in degrees Celsius ?
0K = abolsute zero, the point at which matter has no energy, this is equal to -273 degrees Celsius
Define the radian (rad)
One radian is encloses an arc which has a length equal to the circle radius
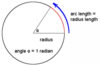
What is the relationship of radians to a full revolution (360 degrees)?
2π radians = a full revolution (360 degrees)
Note for maths purposes ignore the names and have it as 2π = 360
What does pi represent ?
It represents a constant, the ratio of the circumference of a circle to its diameter, it is the same for all circles
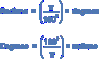
What is the equation for converting between radians and degrees ?
The more formal equation is in page 4 of mechanics binder
What is the difference between scalar and vector quantities
A scalar is a quantity that has a magnitude only
A vector is a quantity that has a magnitude and direction
Describe the difference between distance and displacement
- Distance is simply the total distance travelled regardless of direction; it is a scalar quantity
- Displacement is a straight-line distance and a defined direction; it is a vector quantity
Describe the difference between angular distance and angular displacement
- An angular distance is simply the total angle turned through
- Whereas angular displacement has a magnitude (the angle it is turned through) and direction (the direction of the rotation about an axis); it is a vector quantity e.g. consider a bath tap if you instructed someone to turn a bath tap you would tell them both the direction and the angle through which to turn it
How are scalar quantities added together ?
They can be added using simple rules of arithmetic, there is nothing new to learn for this
e.g. 1kg + 2kg = 3kg
What are the two main methods for adding or subtracting vectors together ?
- Combining vectors graphically
- Resolving using trigonometry
What is the term used to describe the vector produced when two or more vectors are added or subtracted ?
The resultant vector
Describe the basic idea behind using trigonometry for resolving vectors
- The basic idea is to replace each vector with a pair of vectors ar right-angles to each other.
- This is called resolving the vector into its components, the resolved vectors along each direction can then be added to give the components of the resultant vector
Why do you often work in degrees when using trigonometry when the SI unit for angles is radians ?
Because it is easier to visualise degrees and calculators are naturally set to work in degrees not radians
Which is the preferred method for combining vectors ?
Using trigonometry
Look over pages 8&9 in binder to see the worked examples of resolving vectors using trigonometry
What are all positions and directions in mechanics and biomechanics given in relation to ?
A reference frame
The choice and position of the reference frame will be dependent upon the movement being studied. For example, if you are interested in the movement of someone walking then you will probably use a reference frame fixed on the ground. However, if you were interested in how the head moves during walking then you may choose the reference frame to be fixed on the trunk.
When the position and motion of objects are stated, it is important that they are given in relation to some kind of reference frame, the positions within a reference frame need to be related, this is done with a co-ordinate system, what are the 2 main co-ordinate systems we should know about ?
- The rectangular co-ordinate system
- The polar co-ordinate system
Describe the basic three-dimensional rectangular co-ordinate system
This is the Caresian system - it consists of three axis at right angles to each other, normally labelled as x, y & z axis. A simple way to imagine this is as three edges of a cube.
For a three-dimensional system, three co-ordinates (x, y, z) give the position of a point. The co-ordinates of the origin (the point where all axes cross) are (0, 0, 0)
What are the axes in a rectangular co-ordinate system when considering 2 dimensions?
The x and y axes
Go over the worked example on Pg. 11 in the binder for Cartesian systems
When axes are all at right angles to each-other, as in the cartesian system what are they said to be ?
They are said to be orthogonal
What is special about orthogonal axes ?
They are independent of each other; a change in position on one axis does not result in a change in position on another one
e.g. imagine yourself travelling along the x-axis, your position on that axis will change but your position on the y & z axes will remain the same.
Describe what a plane is in maths
A plane is a flat surface (like a thin sheet of paper) it is regarded as having zero thickness and is therefore two-dimensional
Pic below shows 3 different planes
Here are some facts about planes that are important to remember:
- Two planes can be at right-angles to each other
- Three planes but no more, can mutually be at right angles, as at the corner of a cube
- A straight line is formed where two planes cross each other
Are angles given in the cartesian co-ordinate system ?
No - this doesn’t mean it couldn’t be calculated however
What is the main difference between polar co-ordinates and rectangular co-ordinates ?
In polar co-ordinates angles are also used to describe positions
Describe what is meant by polar co-ordinates
In 2-D this means giving the angle of the line and its length (rc, θc) Look at the worked example on Pg 14
In 3-D this means giving a distance and 2 angles (r, θ, ϕ) look at the example on Pg 15
When are polar co-ordinates more useful than rectangular co-ordinates ?
In studies of circular objects and when angles and rotations are important.
In biomechanics, polar co-ordinates can be useful in describing the motion of joints. For example, in the sagittal plane (two dimensions only) the position of the knee joint can be described relative to the trunk using an angle and a length. In this case, the angle describes the flexion and extension of the hip joint and the length describes the length of the thigh.
What term is used to describe the movement of an object in a circular path around an axis with no translation taking place ?
A rotation
What is kinematics ?
This is the study of motion (or movement), it is concerned with the ways in which objects move but not with the causes of movement (the causes of movement are forces)
What is the two distinct ways in which movement can occur ?
- A linear (or translational) motion
- A rotary (or rotational) motion
An object can only undergo linear or rotatory motion but not at the same time - T or F?
False - An object may undergo either linear or rotary motion or both at the same time.
e.g. a car travelling along a straight road is undergoing linear motion, a windmill rotating about its central axis is undergoing rotary motion, and a football rolling along the ground moves in a straight line and rotates as well - it is undergoing both linear and rotary motion at the same time.
What type of movement can joints undergo
Joints may only undergo rotary motion, rotating about the joint centre, yet by working together the joints can result in an overall linear motion.
e.g. during walking the combined rotations of the joints of the lower limbs result in overall linear motion
Describe what is meant by the term movement constraints
This is when an object has limited movements
- e.g. you could have a cup in your hand which you can move up and down, forward and back, and from side to side. You can also rotate the cup in any way thus the cup is free to move in all possible ways.
- On the other hand you could have a door which is only free to rotate about an axis through its hinges, this is termed constrainted movement
What term is used to describe the movement of an object in a straight line with no rotation ?
A translation
(think of this with reference to a cartesian system)
