Maths required

Question 1

How do you go about solving a second order ODE?

Answer 1

Use the auxilliary equation am²+bm+c=0 to find a value of m.

Question 2

What are the three different solutions for the auxilliary equation for a second order ODE?

Answer 2

1) Real and different roots (m=m₁ and m=m₂)

y=Ae^m₁x+Be^m₂x

2) Real and equal roots (m=m₁=m₂)

y=e^m₁x(A+Bx)

3) Complex roots (m=w+/-jP)

y=e^wx(AcosPx+BsinPx)

Question 3

Which special case solution often comes up in transport processes?

Answer 3

Question 4

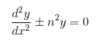
What are the two common solutions to the special case 2nd order ODE?

Answer 4

1) if a=1, b=0 and c=n², then m=sqrt(-n²)=+/-jn

therefore y=e^wx(AcosPx+BsinPx), in this case w=0 and P=n

therefore y=Acosnx+Bsinnx

2) if a=1, b=0 and c=-n², then m=+/-n, so m₁=n and m₂=-n

therefore y=Ae^m₁x+Be^m₂x=Ae^nx+Be^-nx=Acoshnx+Bsinhnx