Diffusion

Question 1

State Fick’s law.

Answer 1

Question 2

Draw a small control volume for diffusivity and construct the general mass balance.

Answer 2

See footnote 38.

Question 3

Simplify the differential equation for transient diffusion using a simalarity variable.

Answer 3

See footnote 39.

Question 4

Solve the simplified differential equation for transient diffusion.

Answer 4

See footnote 40.

Question 5

Apply the boundary conditions to the simplified equation for transient diffusion, and change the resulting equation back to the original variables.

Answer 5

See footnote 41.

Question 6

Derive the equation for mass flux at the surface of a transient diffusion situation.

Answer 6

See footnote 42.

Question 7

Derive the equation for total mass transfer per unit area for transient mass diffusion.

Answer 7

See footnote 43.

Question 8

Draw a diagram to represent gas dissolution in a falling film.

Answer 8

See footnote 44.

Question 9

Draw the control volume for dissolution of gas in a falling film.

Answer 9

See footnote 45.

Question 10

Construc the mass balance for gas dissolution in a falling film and state the boundary conditions.

Answer 10

See footnote 46.

Question 11

Simplify the differential equation for mass dissolution through a falling film using a simalarity variable.

Answer 11

See footnote 47.

Question 12

Solve the differential equation for gas dissolution into a falling film.

Answer 12

See footnote 48.

Question 13

Apply the boundary conditions to the simplified version of the equation for mass dissolution through a falling film and convert it back to it’s original variables.

Answer 13

See footnote 49.

Question 14

Derive the equation for the surface flux of dissolution through a falling a falling film.

Answer 14

See footnote 50.

Question 15

Derive the equation for the total rate of absorption for mass dissolution through a falling film.

Answer 15

See footnote 51.

Question 16

Draw a diagram for a gas (A) absorbing into a liquid (B) that reacts to the reaction A+B=AB

Answer 16

See footnote 52.

Question 17

Draw a control volume for gas diffusing into a liquid to a reaction A+B=AB

Answer 17

See footnote 53.

Question 18

Construct the mass balance for gas diffusing into a liquid with the reacter A+B=AB and state the boundary conditions.

Answer 18

See footnote 54.

Question 19

Use non-dimensionalised variables to simplify the mass balance for gas diffusing into a liquid with a reaction.

Answer 19

See footnote 55.

Question 20

What is the Thiele modulus?

Answer 20

Question 21

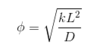
Solve the differential equation in terms on non-dimensional variables for gas diffusion into a liquid with a reaction.

Answer 21

See footnote 56.

Question 22

Apply the boundary conditions to the equation with non-dimensionalised variables to find the constants and return the equation to the original variables.

Answer 22

See footnote 57.

Question 23

What happens to the Thiele modulus when reaction rate increases?

Answer 23

It increases

Question 24

What happens to the Thiele modulus when diffusion rate increases?

Answer 24

It decreases

Question 25

Draw a graph to show how conversion changes with fraction of the length for mass diffusion with a reaction in terms of Thiele modulus.

Answer 25

Question 26

Derive the equation for average concentration for diffusion with a reaction.

Answer 26

See footnote 58.

Question 27

Derive the flux for the surface of gas diffusion into a liquid with a reaction

Answer 27

See footnote 59.