Market Risk Measurement and Management Flashcards
The relationship between arithmetic rt and geometric Rt returns using a Taylor’s series expansion for the natural log
Empirical and estimated VaR
Lognormal VaR
Delta-normal VaR
- Delta-normal VaR assumes that:
- returns are normally distributed (or multivariate normal)
- [delta] the portfolio/position exposures, to the risk factor(s), are expressed linearly
Sprectral risk measure
A spectral risk measure is a risk measure given as a weighted average of outcomes where bad outcomes are included with larger weights
Age-weighted historical simulation (Boudoukh, Richardson and Whitelaw approach (BRW))
- The data is weighted using a weighting function
- w(1) = w(1)
- w(2) = λw(1)
- w(3) = λ2w(1)
- …
Volatility-weighted historical simulation (Hull and White (HW))
- rt,i = the return of asset i on day t
- σt,i = the estimated volatility on day t
- σT,i = the most recent estimation of volatility
Filtered historical simulation advantages
- It enables us to combine the non-parametric attractions of HS with a sophisticated (e.g., GARCH) treatment of volatility, and so take account of changing market volatility conditions.
- It is fast, even for large portfolios.
- As with the earlier HW approach, FHS allows us to get VaR and ES estimates that can exceed the maximum historical loss in our data set.
- It maintains the correlation structure in our return data without relying on knowledge of the variance-covariance matrix or the conditional distribution of asset returns.
- It can be modified to take account of autocorrelation or past cross-correlations in asset returns.
- It can be modified to produce estimates of VaR or ES confidence intervals by combining it with an OS or bootstrap approach to confidence interval estimation.
- There is evidence that FHS works well.
Risk axiomes
Average correlation between n assets
Market risk consists of four types of risk
- Equity risk
- Interest-rate risk
- Currency risk
- Commodity risk
Credit migration
The risk that the credit quality of a debtor decreases
Joint probability of default for two binomial events
Standard deviation of a binomially distributed variable X
CVaR credit value-at-risk
Measures the maximum loss of a portfolio of correlated debt with a certain probability for a certain timeframe
DV01
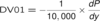
Arbitrage-free models
Models that take the initial term structure as given
Equilibrium models
Models that start with assumptions about the interest rate process and about the risk premium demanded by the market for bearing interest rate risk and then derive the risk-neutral process
Risk-neutral process with drift
- λ = drift term
- dr denotes the change in the rate over a small time interval dt, measured in years
- σ denotes the annual basis-point volatility of rate changes
- dw denotes a normally distributed random variable with a mean of zero and a standard deviation of dt1/2
Risk-neutral process with time-dependant drift (Ho-Lee model)
- λ = drift term
- The drift of the interest rate process is presumed to be time-varying.
- No long-run equilibrium value is defined in the Ho-Lee model.
Risk-neutral process with time-dependant volatility
Standard deviation of the change in rate
Tree approximating a risk-neutral process with drift
Tree approximating a risk-neutral process with time-dependant drift
The risk-neutral dynamics of the Vasicek model
- θ denotes the long-run value or central tendency of the short-term rate in the risk-neutral process
- k denotes the speed of mean reversion
- The Vasicek model incorporates mean reversion. The flexibility of the model also allows for risk premium, which enters into the model as constant drift or a drift that changes over time.
Risk-neutral process with volatility as a function fo the short-rate (Cox-Ingersoll-Ross (CIR) model)
- The annualized standard deviation of dr (i.e., the basis-point volatility) is proportional to the square root of the rate. The basis-point volatility of the short rate is not independent of the short rate as other simpler models assume.
- Short-term rate in the CIR model cannot be negative because of the combined property that (i) basis-point volatility equals zero when short-term rate is zero, and (ii) the drift is positive when the short-term rate is zero.
Put-call parity
Weighted expected short-fall (WES)
- λ is set by the Basel Committee to be 0.5
- EST is the expected shortfall calculated for the total portfolio
- ESPj is jth partial expected shortfall
Expected Shortfall
- If the average of the sum of all VaR above the threshold level
Basel profit and loss attribution 2 measures
- U denotes the difference between the actual and model profit/loss in a day
- V denotes the actual profit/loss in a day
FRTB 2 types of credit risk
- Credit spread risk is the risk that the company’s credit spread will change, causing the mark-to-market value of the instrument to change.
- Jump-to-default risk is the risk that there will be a default by the company.
FRTB change from VaR to ES
After 20 years of using VaR with a 10-day time horizon and 99% confidence to determine market risk capital, regulators are switching to using ES with a 97.5% confidence level and varying time horizons
Risk premium of duration
Is added only on the rate futher than the first period on the interest rate tree
Number of days where the VaR exceeds threshold
- The binomial distribution can be used to test whether the number of exceptions is acceptably small.
- x is the number of occurrence
- p is the left tail probability
- T is the number of periods
Fixed-income mapping
- With principal mapping, one risk factor is chosen that corresponds to the average portfolio maturity. Considers the timing of redemption payments only.
- With duration mapping, one risk factor is chosen that corresponds to the portfolio duration. A portfolio is replaced by a zero-coupon bond with maturity equal to the duration of the portfolio.
- With cash-flow mapping, the portfolio cash flows are grouped into maturity buckets. Considers the correlation among zero-coupon bonds.
- Mapping should preserve the market value of the position. Ideally, it also should preserve its market risk.
Risk-neutral probability of default
PV = [(1 - λ) * value if not default + λ * value if default] * e-rt
Implied distribution vs lognormal distribution impact on option prices
- The implied distribution of the underlying equity prices derived using the general volatility smile of equity options has a heavier left tail and a less heavy right tail than a lognormal distribution of underlying prices. Therefore, using the implied distribution of prices causes deep-out-of-the-money call options on the underlying to be priced relatively low compared with using the lognormal distribution.
- The implied distribution of underlying foreign currency prices derived using the general volatility smile of foreign currency options has heavier tails than a lognormal distribution of underlying prices. Therefore, using the implied distribution of prices causes deep-out-of-the-money call options on the underlying to be priced relatively high compared with using the lognormal distribution.
Extreme Value Theory (EVT) key results
- A key foundation of EVT is that as the threshold value is increased, the distribution of loss exceedances converges to a generalized Pareto distribution. Assuming the threshold is high enough, excess losses can be modeled using the generalized Pareto distribution. It is known as the Gnedenko–Pickands–Balkema–deHaan (GPBdH) theorem and is heavily used in the peaks-over-threshold (POT) approach.
- If the tail parameter value of the generalized extreme-value (GEV) distribution goes to zero, and not infinity, then the distribution of the original data (not the GEV) could be a light-tail distribution such as normal or log-normal. In other words, the corresponding GEV distribution is a Gumbel distribution.
- To apply EVT, the underlying loss distribution can be any of the commonly used distributions: normal, lognormal, t, etc.
- As the threshold value is decreased, the number of exceedances increases.
Liquidity Duration
The number of days it would take to dispose of a certain number of shares
Liquidity adjusted VaR
= ((bid-ask spread in %) / 2 * dollar value of the position) + VaR
