Magnetism

Question 1

Give the equation for M, the magnetisation of a material in a magnetic field H

Answer 1

X_m is the magnetic susceptibility, ie how magnetic the material is per unit volume

Question 2

Give the equation for the magnetic susceptibility per gram

Answer 2

Note that p is the density of the material

Question 3

Give the equation for the molecular susceptibility

Answer 3

Question 4

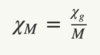
Define diamagnetism

Answer 4

A diamagnetic material is one which tends to repel the applied field, ie forms a magnetic field in the opposite direction to the one applied. Diamagnetism arrises due to the circulation of electron pairs within an atom. All electrons are paired up.

χ < 0 for a diamagnetic material

Question 5

Define paramagnetism

Answer 5

When samples are placed in a magnetic field, you may find that they are magnetised in the same direction as the applied field. This is called paramagnetism and is due to the material containing unpaired electrons - radicals.

Question 6

State and describe the Curie law

Answer 6

Spins in a material are subject to thermal motion. The magnitude of magnetic susceptibility, therefore, depends on temperature.

Pierre Curie discovered that for paramagnetic materials, X is inversely proportional to T

Question 7

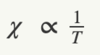
Describe a material if χ > 0

Answer 7

For any material, its core electrons will exhibit diamagnetic behaviour, and any unpaired valence electrons will exhibit paramagnetic behaviour.

Question 8

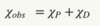
Describe how to count unpaired electrons

Answer 8

Question 9

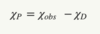
Describe the magnetic moment μ_eff

Answer 9

μ_eff tells us how strong each individual molecular magnet is

Question 10

Give the spin only formula

Answer 10

S is the spin quantum number

Question 11

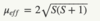
Give the spin only formula using n instead of S

Answer 11

Where n is the number of unpaired electrons

Question 12

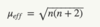
Give the three conditions for an orbital contribution to the magnetic moment to be observed for the first row of transition metals

Answer 12

1. You must have degenerate orbitals or orbitals of very similar energy
2. There must be an electronic degeneracy - you could have the same number of unpaired electrons but arranged in different orbitals
3. The orbitals must have similar shapes but different orientations so that when you move from one to the other you get a rotation around an axis