Line and surface integrals Flashcards
(23 cards)
Define a regular arc.

Define a regular curve.
A regular curve consists of a finite arcs joined end to end.
What is the following called and how else can we denote it?
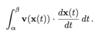
The line integral of v along the arc C
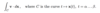
Does the line integral depend on the choice of parametrisation of C?
No
If the integral is done over a regular closed curve how do we denote the integral?
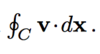
What is the formula for the length of a curve, C via integration.
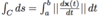
What is the formula to find the mass, if f is a density funciton, via integration?
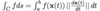
What is the formula to find the work done, if F is a force, via integration?

What parametrisation would you use for the following?
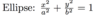

What parametrisation would you use for the following?


What parametrisation would you use for the following?
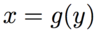
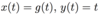
What parametrisation would you use for the following?


What are the four steps to perform a line integral?

How would you modify the following for regular curves?

To the steps for each arc, and then add up the results
What is the first method to specify a surface?
Method 1 - Give the surface in parametric form and
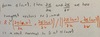
What is the parametrisation for spherical (polar) coordinates?

What is the parametrisation for a cylinder, radius a, centred on z-axis.

What is the unit vector normal to the surface S at x(u,v)?
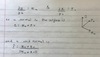
What is the definition of the surface integral as limit?

What is the integral over a surface equal to using method 1 - where the surface is specified in parametric form?
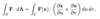
What is the integral over a surface equal to when using method 2 - where S is given as a level set.
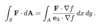
What has the following formula converted a sufrace integral into?
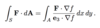
Integral over A, projection of S into the xy plane.
What is the second method to specify a surface?



