Green's, Stokes' and Divergence theorems. Flashcards
(30 cards)
What is Green’s theorem in the plane?

How can you write Green’s theorem in the plane in vector form?

What is Stokes’ theorem a generalisation of?
Green’s theorem to arbitrary surfaces
What is Stoke’s theorem?

What is the divergence theorem?

What are these three theorems extensions of?
The fundamental theorem of calculus.
What is an important application of the divergence theorem?
Conservation laws and the continuity equation.
What is an interpretation of the following?
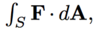
The flux of some quantity F through the surface of interest.
What is flux?
Flux is the rate of flow per unit area
Which way is flux measured?
Perpendicular to the face of the surface
How is flux related to dA?
Flux is dA multiplied by the unit normal vector ň
What are fives fluxes?
- Magnetic flux (F = B)
- Electric fluc (F = E)
- Transport fluxes such as mass (F = ρv)
- Heat
- Energy
What is the continuity equation?

What is an application of Stoke’s theorem?
Path independence of line integrals.
What is a conservative vector field?
Vector fields for which the line integral is path independent.
Define simply connected.`

If D is simply connected what does the imply about path independence?

If ∇ x F is zero in some region D what does this imply about F?
F is the gradient of the scalar field there.
F = ∇ɸ
What is the funciton ɸ called?
The scalar potential
Prove that when you start with F = ∇ɸ you can show path independence directly.

How does path indepence, ∇ x F = 0 and the scalar potential relate?

What does j stand for in the following continuity equation?

j = ρv, which is the flux
If the closed curve is the boundary of a surface S, and if ∇ x F = 0 on S than what is the following equal to?

0 - no need to do the surface integral
A change in variables is also known as?
A change in coordiante system






