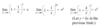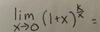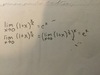Limits

Question 1

What is the intuitive (informal) definition of a limit?

Answer 1

If f(x) becomes arbitrarily close to a single number “L” as x approaches “a” both from the right and left sides, then the limit of f(x) as “x” approaches “a” is “L” and written as shown.

Question 2

What is the definition of a one-sided limit?

Answer 2

Question 3

When does a limit exist?

Answer 3

Question 4

When does a limit fail to exist?

Answer 4

Limits fail to exist:

1. If either of the one-sided limits DNE
2. If the one-sided limits are unequal
3. If either of the limits is unbounded (“L” approaches infinity as “x” becomes very close to “a”).

Question 5

Explain some of the most crucial Theorems for Basic Limits.

Answer 5

Theorems for Basic Limits:

1. If x=c is in the domain of f(x) (i.e. if f(x) is defined at x=c) then the limit of f(x) as “x” approaches “c” can be solved via direct substitution.
2. The limit of a constant is the constant itself (regardless of the “x” value of which you are taking the limit (i.e. the limit of f(x) as “x” approaches “a” of constant “k” = “k”.
3. The limit of a variable is the value for “x” of which you are taking the limit (i.e. the limit of f(x) as “x” approaches “a” of variable “x” = “a”.

Question 6

Explain the sum law of limits supposing all limits exist.

Answer 6

The limit of a sum is the sum of the limits.

Question 7

Explain the difference law of limitis supposing all limits exist.

Answer 7

The limit of a difference is the differences of the limits.

Question 8

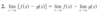
Explain the constant multiple law of limits supposing that “c” is a constant and that all limits exist.

Answer 8

The limit of a constant times a function is the constant times the limit of the function.

Question 9

Explain the product law of limits supposing all limits exist.

Answer 9

The limit of a product is the product of the limits.

Question 10

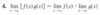
Explain the quotient law of limits supposing all limits exist.

Answer 10

The limit of a quotient is the quotient of the limits (provided that the limit of the denominator is not 0).

Question 11

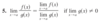
Explain the power law of limits supposing all limits exist.

Answer 11

Question 12

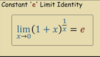
Explain some additional special limits.

Answer 12

Question 13

Explain the root law of limits supposing all limits exist.

Answer 13

Question 14

Note another theorem (properties of limits).

Answer 14

• Let “b” and “c” be real numbers.
• Let “n” be a positive integer
• Let “f” and “g” be functions with limits
• The limit of f(x) as “x” approaches “c” = L
• The limit of g(x) as “x” approaches “c” = K

Question 15

Explain the direct substitution property of limits.

Answer 15

Question 16

What is true if f(x) = g(x) when x ≠ a?

Answer 16

Question 17

Note another theorem of limits.

Answer 17

Question 18

Explain the greatest integer function.

Answer 18

Question 19

Explain the composition rule of limits.

Answer 19

Question 20

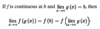
Explain the natural logarithm rule of limits.

Answer 20

Question 21

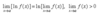
Explain the strategy for finding limits.

Answer 21

1. Check if “c” is in the domain of f(x) an if f(x) is continuous at x=a.
   
   • If so, then the limit of f(x) as “x” approaches “c” = f(c).
2. Otherwise, try the dividing out technique
   
   • Factor both the numerator and the denominator completely and simplify the common factors.
3. Rationalism
   
   • Rationalize the numerator or the denominator by multiplying with the conjugate of N(x) or D(x).

Question 22

Explain the Squeeze Theorem.

Answer 22

Question 23

Note an important limit theorem.

Answer 23

Question 24

Explain the precise definition of a limit.

Answer 24

Question 25

What is the limit of sin(kθ)/θ as θ approaches 0?

Answer 25

The limit of sin(kθ)/θ as θ approaches 0 = k

Question 26

What is the limit of sin(kθ)/sin(pθ) as θ approaches 0?

Answer 26

The limit of sin(kθ)/sin(pθ) as θ approaches 0 = k/p, provided that p≠0.

Question 27

Note one of three important trigonometric limits.

Answer 27

Question 28

Note one of three important trigonometric limits.

Answer 28

Question 29

Note one of three important trigonometric limits.

Answer 29

Question 30

What is the limit of tan(kθ)/θ as θ approaches 0?

Answer 30

The limit of tan(kθ)/θ as θ approaches 0 = k

Question 31

What is the limit of tan(kθ)/tan(pθ) as θ approaches 0?

Answer 31

The limit of tan(kθ)/tan(pθ) as θ approaches 0 = k/p, provided that p≠0.

Question 32

Describe the constant “e” limit identity.

Answer 32

Note: if you add a constant in front of “x” (replacing “x” with “k*x” then the limit becomes e^k .

i.e. the limit of (1+kx)^1/x as “x” approaches 0 = e^k

Question 33

Note some important limits.

Answer 33

Question 34

What is the following limit?

Answer 34