Leetcode 4 Flashcards
(11 cards)
Generate Parentheses
Brute force is to just try all 2^(2n) combinations and then validate each sequence, which takes O(n) time. Can improve on this by only adding a ")" if it doesn't invalidate the sequence. Backtracking w/ Recursion -\>
public List generateParenthesis(int n) {
List list = new ArrayList();
backtrack(list, "", 0, 0, n);
return list;
}
public void backtrack(List list, String str, int open, int close, int max){
if(str.length() == max*2){
list.add(str);
return;
}
if(open < max)
backtrack(list, str+”(“, open+1, close, max);
if(close < open)
backtrack(list, str+”)”, open, close+1, max);
}
}
}
Time: For recursion tree, it’s a binary tree with tree node representing an unfinished string. The two tree branches are either “(“ or “)”, representing the character to be appended to the string. To find all valid strings, need to traverse whole tree till height 2n. So O(2^(2n)) = O(4^n)
Space: same
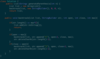
Word Break (s = leetcode, worddict = [“leet”, “code”] -> true
DP: boolean[] f = new boolean[s.length() + 1] where f[i] indicates whether subarray(0, i) can be segmented into words from the dict. f[0] = true; (default value is false)
boolean[] f = new boolean[s.length() + 1];
f[0] = true;
for(int i = 1; i <= s.length(); i++){
for(String dictionaryWord: wordDict){
int lengthOfWord = dictionaryWord.length();
if (lengthOfWord <= i) {
boolean canMakeWordUpToThisPoint = f[i - lengthOfWord];
if (canMakeWordUpToThisPoint) {
String substringContinuedFromLastCompleteWord = s.substring(i - dictionaryWord.length(), i);
if (substringContinuedFromLastCompleteWord.equals(dictionaryWord)) {
f[i] = true; // Can make a word from the last point to here
break; // No need to look at more words, we found a continuation
}
}
}
}
}
return f[s.length()];
Time: two nested loops with substring computation -> O(n^3)
Space: O(n) length of f
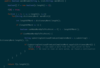
Happy Number (replacing number by the sum of the squares of its digits)
qfollowing the pattern leads to 1) it gets to 1, 2) it gets stuck in a cycle, 3) it goes higher and higher up to infinity. For third possibility, note that a number with 3 digits will never go larger than 243, so it must get stuck in a cycle below 243 or go to 1. Numbers with 4 or more digits will always lose a digit at each step until they are down to 3 digits.
Helper = calculate next number
public int calculateNext(int x) {
int currentSum = 0;
while (x > 0) {
int onesDigit = x % 10;
currentSum += Math.pow(onesDigit, 2);
x = x / 10;
}
return currentSum;
}
public boolean isHappy(int n) {
Set numberList = new HashSet<>();
while (n != 1 && !numberList.contains(n)) {
if (n < 243) {
numberList.add(n);
}
n = calculateNext(n);
}
return n == 1;
Time: O(logn) for numbers below 243, wont take more than 243 steps to terminate. For numbers above 243, worst case each cost is O(logn) + O(loglogn) + O(logloglogn) etc which is O(logn)
Space: O(logn) without only saving numbers in HashSet that are less than 243, space is O(243*3) = O(1) by not saving them

Product of Array Except Self (without / operator)
Note that productExceptSelf[i] is the product of all to left and all to right. First loop through array and create result[] array which will be the final result but for now holds products of all numbers to the left of i for result[i]. Then, loop through the array starting from the end and check if i < n-1 and use one var right = right * nums[i+1] and set result[i] = result[i] * right;
int n = nums.length;
int[] res = new int[n];
res[0] = 1;
for (int i = 1; i < n; i++) {
res[i] = res[i - 1] * nums[i - 1];
}
int right = 1;
for (int i = n - 1; i >= 0; i–) {
res[i] *= right;
right *= nums[i];
}
return res;
Time: O(n), Space: O(1) not counting the output array
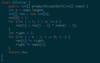
Valid Sudoku
Use a HashSet to track seen numbers, then use simple string assignments such as “num + ‘r’ + i”, etc
public boolean isValidSudoku(char[][] board) {
Set seen = new HashSet();
for (int i=0; i<9; ++i) {
for (int j=0; j<9; ++j) {
char number = board[i][j];
if (number != ‘.’)
if (!seen.add(number + “ in row “ + i) ||
!seen.add(number + “ in column “ + j) ||
!seen.add(number + “ in block “ + i/3 + “-“ + j/3))
return false;
}
}
return true;
Time and Space are both constant due to size of board being 81 cells but worst case for both is O(n^2) and O(n^2) in case whole board is valid
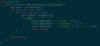
Longest Palindromic Substring
DP: use boolean[][] dp = new boolean[n][n] where dp[i][j] indicates if substring s starting at index i and ending at j is palindrome. Two for-loops starting at the end because each check depends on dp[i+1][j-1]
int n = s.length();
String res = null;
int palindromeStartsAt = 0, maxLen = 0;
boolean[][] dp = new boolean[n][n]; // dp[i][j] indicates whether substring s starting at index i and ending at j is palindrome
for(int i = n-1; i >= 0; i–) {
for(int j = i; j < n; j++) {
dp[i][j] = (s.charAt(i) == s.charAt(j)) // chars at i and j should match
&&
( j-i < 3
|| dp[i+1][j-1] );
//update max palindrome string
if(dp[i][j] && (j-i+1 \> maxLen)) {
palindromeStartsAt = i;
maxLen = j-i+1;
}
}
}
return s.substring(palindromeStartsAt, palindromeStartsAt+maxLen);
Time: O(n^2) Space: O(n^2) to store the table
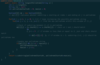
Container With Most Water
Two pointer approach: Start at both ends, area between pointers is Min(both heights)*(distance between two pointers). Track greatest height going along, update when necessary. Note that if height of i and j are equal, it doesnt matter which one we move inward.
int greatestArea = 0;
int i = 0;
int j = height.length - 1;
while (i != j) {
int smallerHeight = Math.min(height[i], height[j]);
int distance = j - i;
int localArea = smallerHeight * distance;
greatestArea = Math.max(greatestArea, localArea);
if (height[i] > height[j]) {
j –;
}
else {
i ++;
}
}
return greatestArea;
Rough proof: going from the widest container, all others are less wide and therefore must have a higher water level to hold more water. The initial smaller height can’t support a higher water level and can thus be removed form consideration (by moving that pointer inwards).
Time: O(n), Space: O(1)

Search in Rotated Sorted Array
One pass binary search. If middle pivot is not equal to target, and it’s greater than nums[left], then left part is sorted. Else, right part is sorted. Then proceed with BS as usual.
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left \<= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid] \>= nums[left]) {
if (target \>= nums[left] && target \< nums[mid]) right = mid - 1;
else left = mid + 1;
}
else {
if (target \<= nums[right] && target \> nums[mid]) left = mid + 1;
else right = mid - 1;
}
}
return -1;
Time: O(logn), Space: O(1)
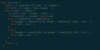
Rotate an array around an index k
Reverse the array k times in the following order: reverse whole array, reverse first k numbers, reverse last n-k numbers.
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end–;
}
}
Time: O(3*n) = O(n), Space: O(1)
Longest Substring Without Repeating Characters
hashmap with k:v -> char in string : index in string. This way we don’t need to clear HashMap after duplicates are found b/c we can tell whether a previously seen character was seen in the current substring we’re on or not.
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map map = new HashMap\<\>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j \< n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j)), i);
}
ans = Math.max(ans, j - i + 1);
map.put(s.charAt(j), j + 1);
}
return ans;
}
Time: O(n) Space: O(min(m, n)) where n is length of the string, m is the size of the charset/alphabet. This is because all duplicate characters are entered in the HashMap, overriding their prev entires. so “ababab” HashMap has size 2

Roman to Integer
Hardcode all single and double Roman Numerals into a HashMap I, V, X, L, C, D, M, IV, IX, XL, XC, CD, CM with values (String : Integer)
set sum, i = 0; while i < s.length(), check if i < s.length() - 1, then string = s.substring(i, i+2), check if string is in Map. If so, update sum by map(string), i += 2; continue;
otherwise, it must be 1 string so singleSymbol = s.substring(i, i+ 1) sum+= values.get(singleSymbol), i+= 1
Time: O(1) due to finite set of roman numerals. Max Value can be 3999 which is MMMCMXCIX. Space: O(1) b/c HashMap has constant number of entries



