Leetcode 2

Question 1

3Sum (all triplets that add to 0) with Sorting

Answer 1

Sort the input Array. Iterate through the Array, if current val > 0, break. Otherwise, call twoSum on current position i.

public List> threeSum(int[] nums) {
Arrays.sort(nums);
List> res = new ArrayList<>();
for (int i = 0; i < nums.length && nums[i] <= 0; ++i)
if (i == 0 || nums[i - 1] != nums[i]) {
twoSumII(nums, i, res);
}
return res;
}
void twoSumII(int[] nums, int i, List> res) {
int lo = i + 1, hi = nums.length - 1;
while (lo < hi) {
int sum = nums[i] + nums[lo] + nums[hi];
if (sum < 0) {
++lo;
} else if (sum > 0) {
–hi;
} else {
res.add(Arrays.asList(nums[i], nums[lo++], nums[hi–]));
while (lo < hi && nums[lo] == nums[lo - 1])
++lo;
}
}
}

Time: O(n^2). TwoSum is O(n) and we call it n times. Sorting takes O(nlogn) so overall is O(nlogn + n^2) = n^2
Space: Ignoring memory required for the output, depends on sorting algorithm (with quicksort its O(logn)).

Question 2

3Sum (no sorting allowed)

Answer 2

1) use a hashSet to skip duplicates in the outer loop
2) Add to HashMap indicating if we have encountered that element in the current iteration. In the inner loop, key:value = nums[j] : i

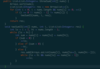
public List\> threeSum(int[] nums) {
 Set\> res = new HashSet\<\>();
 Set dups = new HashSet\<\>();
 Map seen = new HashMap\<\>();
 for (int i = 0; i \< nums.length; ++i)
 if (dups.add(nums[i])) {
 for (int j = i + 1; j \< nums.length; ++j) {
 int complement = -nums[i] - nums[j];
 if (seen.containsKey(complement) && seen.get(complement) == i) {
 List triplet = Arrays.asList(nums[i], nums[j], complement);
 Collections.sort(triplet);
 res.add(triplet);
 }
 seen.put(nums[j], i);
 }
 }
 return new ArrayList(res);
 }

Time: O(n^2) due to two nested loops.
Space: O(n) for the hashset/hashmap, ignoring memory required for the output

Question 3

House Robber

Answer 3

Idea with DP is to decide to rob the current house or skip it so:

go through all houses and keep two counts 1) if we rob this cell, 2) if we didn’t rob this cell. If we rob current cell, prev cell shouldn’t be robbed. so add current val to prev one. If we don’t rob curent cell, then profit is max of prev cell robbed and not robbed. Then update values for next round

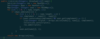
public int rob(int[] nums)
{
int ifRobbedPrevious = 0;
int ifDidntRobPrevious = 0;

for(int i=0; i < nums.length; i++)
{

int currRobbed = ifDidntRobPrevious + nums[i];

int currNotRobbed = Math.max(ifDidntRobPrevious, ifRobbedPrevious);

ifDidntRobPrevious = currNotRobbed;
ifRobbedPrevious = currRobbed;
}

return Math.max(ifRobbedPrevious, ifDidntRobPrevious);
}

Time: O(n), Space: O(1)

Question 4

Rotate Image with rotate 4 cells

Answer 4

Approach 1: rotate each set of 4 cells

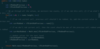
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < (n + 1) / 2; i ++) {
for (int j = 0; j < n / 2; j++) {
int temp = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - j - 1];
matrix[n - 1 - i][n - j - 1] = matrix[j][n - 1 -i];
matrix[j][n - 1 - i] = matrix[i][j];
matrix[i][j] = temp;
}
}
}

Question 5

Letter Combinations of a Phone Number

Answer 5

First, if input is empty, return empty array. Then initiate backtracking with an empty path starting at index 0

In backtrack: if path is the same length as input digits, we have complete combination. Else, get the letters that the current digit maps to, and loop through them. In that loop, add letter to our current path, move on to the next digit, backtrack by removing the letter before moving onto the next

private List combinations = new ArrayList<>();
private Map letters = Map.of(
‘2’, “abc”, ‘3’, “def”, ‘4’, “ghi”, ‘5’, “jkl”,
‘6’, “mno”, ‘7’, “pqrs”, ‘8’, “tuv”, ‘9’, “wxyz”);
private String phoneDigits;

public List letterCombinations(String digits) {
if (digits.length() == 0) {
return combinations;
}

 phoneDigits = digits;
 backtrack(0, new StringBuilder());
 return combinations;
 }

private void backtrack(int index, StringBuilder path) {
if (path.length() == phoneDigits.length()) {
combinations.add(path.toString());
return; // Backtrack
}

String possibleLetters = letters.get(phoneDigits.charAt(index));
for (char letter: possibleLetters.toCharArray()) {
path.append(letter);
backtrack(index + 1, path);
path.deleteCharAt(path.length() - 1);
}
}

Time: O(4^n * n) 4 = max num of digits in a number, which could be 4 for pqrs. Takes n time to construct a string of length n, i.e. path.toString

Question 6

Contains Duplicate

Answer 6

HashSet to check if num in seenNums already 
Set seenNums = new HashSet(); 
 for (int num : nums) { 
 boolean seen = seenNums.add(num); // return True if not present 
 if (!seen) { 
 return true; 
 } 
 } 
 return false; 
Time: O(n), Space: O(n)

Question 7

Best Time to Buy and Sell Stock

Answer 7

Track lowest stock seen so far, overall profit, profit if sold today
int lsf = Integer.MAX_VALUE; // least so far
int op = 0; // overall profit
int pist = 0; // profit if sold today

for(int i = 0; i < prices.length; i++){
if(prices[i] < lsf){ // if we found new buy value which is more smaller then previous one
lsf = prices[i]; // update our least so far
}
pist = prices[i] - lsf; // calculating profit if sold today by, Buy - sell
if(op < pist){ // if pist is more then our previous overall profit
op = pist; // update overall profit
}
}
return op; // return op
Time: O(n), Space: O(1)

Question 8

Valid Parentheses (Different Types)

Answer 8

With a stack:

public boolean isValid(String s) {
 Stack stack = new Stack();
 for (char c : s.toCharArray()) {
 if (c == '(')
 stack.push(')');
 else if (c == '{')
 stack.push('}');
 else if (c == '[')
 stack.push(']');
 else if (stack.isEmpty() || stack.pop() != c)
 return false;
 }
 return stack.isEmpty();
 }

Time: O(n), Space: O(n)

Question 9

Unique Paths (robots on a matrix)

Answer 9

DP: Idea is to use a dp[][] matrix where dp[i][j] is ways to reach that cell. Fill first row/column first because it’s easy (all one). Then loop through the rest of the cells.

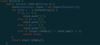
public int uniquePaths(int m, int n) {
 //Boundary case
 if(m \<= 1 || n \<= 1) return 1;

int[][] dp = new int[m][n];

for(int i = 0; i < m; i++){
dp[i][0] = 1;
}

for(int i = 0; i < n; i++){
dp[0][i] = 1;
}

for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}

return dp[m - 1][n - 1];
}

Time: O(m*n) Space: O(m*n). Space can be O(n) with dp = new int[n], Arrays.fill(dp, 1)

int[] dp = new int[n];

Arrays.fill(dp, 1);

for (int i = 1; i < m; i++) {

for (int j = 1; j < n; j++) {

dp[j] = dp[j] + dp[j - 1]; } }

return dp[n - 1];

Question 10

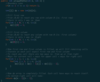
Find First and Last Position of Element in Sorted Array (must be done in O(logn) time

Answer 10

Run Binary Search twice, once to find the lowest index, once to find the highest index. Time: O(logn), Space: O(1)

public int[] searchRange(int[] nums, int target) {

int[] result = new int[2];
result[0] = findFirst(nums,target);
result[1] = findLast(nums,target);
return result;

}

public int findFirst(int[] nums, int target){

int result = -1;
int low = 0;
int high = nums.length - 1;

while(low <= high){
int mid = low + ((high-low)/2);

if (nums[mid] < target){
low = mid + 1;
} else if (nums[mid] > target){
high = mid - 1;
} else { // nums[mid] == target
result = mid;

// because nothing after mid
 // can be the first occurance of target.
 //maybe mid is the first occurance , maybe not
 //so let's narrow the target for [0...mid-1] and find out
 high = mid - 1; 
 //findLast method is exactly the same but with low = mid + 1 instead of the above
 }
 }
 return result;
 }

Question 11

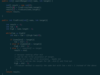
Rotate Image with transpose / reflect

Answer 11

public void transpose(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int tmp = matrix[j][i];
matrix[j][i] = matrix[i][j];
matrix[i][j] = tmp;
}
}
}

public void reflect(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - j - 1];
matrix[i][n - j - 1] = tmp;
}
}
}