Lecture 5: The theory of critical brain dynamics Flashcards
`What is criticality?
A concept where certain materials enter a very special state at the point of a phase transition (as you can see in the picture where Iron undergoes a phase transition from magnetic to non-magnetic at a critical temperature.
What is the difference between scale-free phenomena vs. characteristic scales? Also name examples of both.
Characteristic scales are scales that have a median and mean that overlap (i.e. have a normal distrubution), e.g. apples always have an average size. This in comparison with scale-free phenomena, where mean and median are distant from each other. This means that there’s no typical scale, e.g. a tree (how would you define a branch)?
What is the power-law?
A power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another
When dynamical systems exhibit such type of large variability, they are said to be ‘metastable’ or exhibit ‘critical dynamics’. What is fundamental for identifying critical behaviour?
Identification of power-law statistics (so how does one affect the other).
What are examples of scale-free systems?
Forest fires, financiel markets, earth quakes, rainfall, avalanches.
What is the ‘branching process’ model?
The model for the probability that a unit/neuron passes activity on to its neighbor.
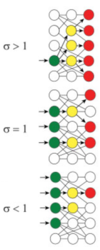
What is the branching parameter?
The ratio of future to past activity.
The branching parameter can either be >1, =1 or <1. Can you explain and what names belong to these ratios?
- A branching parameter of >1 means that 1 neuron (past) will result in firing of (e.g.) 6 neurons (future). The ratio of future to past activity is then 6:1 i.e. >1. This is called super-critical.
- A branching parameter of 1 means that e.g. 3 neurons (past) will result in firing of 3 other neurons (future). The ratio of future to past activity is then 3:3 i.e. 1. This is called critical.
- A branching parameter of <1 means that 5 neurons (past) will result in firing of 1 neuron (future). The ratio of future to past activity is then 1:5 i.e. <1. This is called sub-critical.
What branching pattern is reflected by power-law distribution of avalanche sizes?
The critical branching pattern, with a ratio of 1.
What is meant by the sandpile model?
The fact that a critical slope is an attractor of dynamics. This means that if the slope is shallow, sand can pile up, which increases the slope. And when the slope gets to steep, it will get unstable and an avalanche will occur that releases energy.
What is the theory of self-organized criticality?
Wherever you look in nature, you see complexity (weather systems, mountain ridges, financiel markets etc.). The theory aims to explain why complex systems tend to operate in a distinct balance between order and disorder.
Why is the theory called self-organized criticality?
Computer simulations showed that under a wide range of conditions, the interaction between activity and structure in driven multi-unit systems with non-linear interactions, eventually drags the system to the critical state (as defined by the same spatial and temporal power-law statistics as had been observed many years earlier in spin systems).
What are 4 hallmarks of self-organized criticality?
Driven, many units, nonlinear interactions, long period of self-organization.
How is criticality important for brain function?
Because too little or too much gain of connecting neurons is not beneficial. When the gain is >1, firing of one neuron would lead to firing of thousands of neurons. When the gain is <1, firing of one neuron would not really have an affect at all. Therefore the gain = 1, for homeostatic regulation of synaptic connections in the brain.
What is a white noise spectrum?
A power spectrum generated when a neuronal system is in a super critical state. Here, you can find all sorts of oscillations (slow and fast). The signal looks very noisy. Here, there’s a characteristic amplitude for all frequencies.
What is 1/f spectrum?
Here a transient or metastable pattern is formed that deflects the lower frequencies over the higher frequencies (as you can see by the log graph). Here, the neuronal system is at critical point. Keep in mind that there’s no characteristic amplitude of the different frequency components, but rather a power-law relationship between the amplitudes of different frequencies.
What suggests that LRTC analysis could be used as a biomarker of disease?
Heritability (based on twin studies)
A model with 2500 integrate-and-fire neurons (75% excitatory and 25% inhibitory) arranged in a 2D grid. With background input you can decide how many excitatory neurons fire (25, 50 or 75%). What can be seen from this model?
That neurons only connect within their local range and that excitatory and inhibitory connectivity are independent. With this model, you can recreate a power spectum that looks like a power spectrum derived from EEG data.
What is seen here?
Avalanche-like activity propagation.
Here, a model is displayed where you can combine all sorts of combinations between the amount of inhibitory and excitatory connectivity in a network (right picture). With a color index based on Kappa, you can see what kind of power spectra can be generated (sub-, super- or critical). What does a kappa of 1, <1 or >1 say about criticality?
- Kappa of 1 –> critical (balance of excitatory and inhibitory connectivity)
- Kappa of <1 –> sub-critical (high inhibitory connectivity over excitatory connectivity)
- Kappa of >1 –> super-critical (high exhibitory connectivity over inhibitory connectivity)
Just study this picture and understand it.
Ok
Describe this picture.
The first thing to notice is that oscillations tend to repeat themselves. Furthermore:
- In the sub-critical network very weak and short-lived oscillations, mostly derived from inhibitory activity.
- In the critical network there’s a large variation in oscillation life-time but also in types of oscillations. This makes it very complex.
- In the super-critical network you see sustained long-lasting oscillations (compare it with the critical network).
What do we see when looking at the DFA of a sub- or super-critical network?
That the DFA is close to 0.5, meaning that there’s no temporal structure to the oscillations. The only one with long-range temporal correlations, are the ones in the critical network.
Just know that the balance between inhibitory and excitatory connectivity (E/I balance) for a critical state is equal to the power spectra of a DFA between 0,5-1.
We now know that correlating oscillations can be generated when there’s a balance between inhibitory and excitatory connectivity, so as long as you have e.g. 70% inhibitory connectivity and 30% excitatory connectivity, you get a network at a critical state.
So instead of studying criticality, we actually studied E/I balance.
- What happens when you put in more excitatory connections and look at the amplitude of the oscillations?
- And what happens to the DFA?
- The power/amplitude of the oscillations go up (but based on this you can not determine what the E/I balance should be).
- The DFA goes up to untill it’s at a point that there’s a lot of temporal structure and then goes down again.
Since we know the amplitude of the oscillations goes up when there are more excitatory connections, how could we make use of this to determine the E/I balance?
You can combine the graph with amplitude x structural E/I with the graph with DFA x structural E/I. So you get a graph between DFA and the amplitude (see upper right picture).
From this new graph you can compute a new formula for E/I ratio. What formula is this?
fE/I = 1 - correlation.
So if the correlation is postive (more inhibition), you get a fE/I < 1, which means it is inhibitory dominated. If the correlation is negative (more excitation), you get a fE/I > 1.
