Lecture 4 – Many- atom systems, AIMS and MCTDH

Question 1

• Recap from lecture 3
  
  • Looked at methods for solving the …
  • Born-Oppenheimer: used to find dynamics on single electronic state propagated with DVR/SOFT method
  • Non Born-Oppenheimer: … representation with KE operator controlled coupling converted to diabatic representation controlled by ….
    
    • Former much easier process as … … … … … … (…)
    • latter states as don’t come out of HF and must be diabatised but are overall much more well behaved and … … …. Also propagated with DVR/SOFT method

Answer 1

• Recap from lecture 3
  
  • Looked at methods for solving the TDSE
  • Born-Oppenheimer: used to find dynamics on single electronic state propagated with DVR/SOFT method
  • Non Born-Oppenheimer: adiabatic representation with KE operator controlled coupling converted to diabatic representation controlled by PE.
    
    • Former much easier process as come out of electronic structure calc (HF)
    • latter states as don’t come out of HF and must be diabatised but are overall much more well behaved and easier to process. Also propagated with DVR/SOFT method

Question 2

• Briefly overview both methods the problem with previous methods solving the TDSE and state the two methods that provide a solution

Answer 2

• DVR/SOFT propagation of nuclear/electronic wavefunctions are restricted to 4-5 DOFs (a few atoms)
• To propagate a quantum wavefunction for a many body system must instead use:
  
  • Ab initio multiple spawning (AIMS): practically motivated for very large application-based systems
  • Multiconfiguration time-dependent Hartree (MCTDH): very accurate method that gives close to exact answer.

Question 3

• Describe the from the AIMS method takes in describing the nuclei and electronic state in the time-dependent wavefunction

Answer 3

• Many different nuclear basis functions on different nuclear states all contribute to overall wavefunction with time dependant coefficients define that contribution.

Question 4

• What are the nuclear basis functions that define the AIMS wavefunction?

Answer 4

• Gaussian wavepackets (GWPs) defined by a position and momentum parameter for each DOF.
• Forms many basis functions spread in space but centred in terms of a R/P

Question 5

• What is the key assumption made in AIMS

Answer 5

• Each GWP basis function moves along a classical molecular dynamic’s trajectory independent of other GWP basis functions – no cross talk
• Coefficients c_i^J(t) evolve in time as dictated by TDSE
• Overall this is much easier to simulate

Question 6

• How is the classical MD trajectory formed in AIMS?

Answer 6

• Change in momenta of GWP is a force exerted on the GWP centre which can easily be calculated via electronic structure calculations (e.g. HF/CASSCF)
• Classical MD then used to move GWPS each sitting on an electronic state J (e.g. ES/GS)

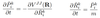
Question 7

How do the coefficients associated with the classical MD trajectory ensure sufficient coupling of states is described?

Answer 7

• An overlap matrix describing overlap between two gaussian as a product (forms a new gaussian)
• Electronic structure and a time overlap matrix combined with this
• Non-adiabatic matrix elements described in Hamiltonian matrix of coefficients

Question 8

• What is the advantage of GWPs?

Answer 8

• Formally integrals were over all space
• GWPs allow local approximations in adiabatic representation
• Data used from ab intio calculations ensures higher accuracy

Question 9

• Explain how AIMS accounts for Cis between states during wavepacket propagation

Answer 9

• Non-adiabatic transitions are included through an adaptive basis set
• Size of basis set (# of Gaussians) is expanded at regions close in energy
• This is done by copies of individual isolated trajectories spawning in the non-starting electronic state at the region of strong non-adiabatic coupling
• Expansion coefficients of these new GWPs starts small but grows over time as more are spawned, increasing probability of transition from ED à Gs in this case

Question 10

• Briefly overview the AIMS process,

Answer 10

• Wavefunction described by GWPs propagating via classical MD trajectories in time the coefficients of which evolve quantumly according to the TDSE
• Many trajectories can be run in parallel
• Adaptive GWP basis growth occurs when non-adiabatic events are detected
• Hamiltonian matrix elements approximated via ab initio calculations

Question 11

Outline the disadvantages of AIMS method

Answer 11

• Classical MD is very efficient but electronic structure calculation of forces is expensive.
• Trajectroy assumption is a big one, preventing quantum-mechanical effects (e.g. tunnelling) being observed correctly
• GWP evolution is approximate, therfore energy conservation not guarenteed

Question 12

• What is an alternative approach to AIMS that does not suffer from the same downfalls?

Answer 12

• Multiconfiguration time-dependent Hartree (MCTDH) method
• No approximations made here that go beyond numerical convergence control

Question 13

• Outline the MCTDH process

Answer 13

• Wavefunction ansatz is a tensor product
• This is a product of many single particle functions (SPFs) with corresponding time-dependent coefficients
• Each SPF is expanded in an underlying TD basis of DVR functions.
• All SPF combinations are combined and multiplied along each DOF and summed to give wavefunction.

Question 14

• Substituting in to … allows derivation of … … for expansion coefficients and SPFs
• Resulting wavefunction is numerically … when sufficient … included on each DOF

Answer 14

• Substituting in to TDSE allows derivation of exact EOMs for expansion coefficients and SPFs
• Resulting wavefunction is numerically exact when sufficient SPFs included on each DOF

Question 15

• What are the disadvantages of MCTDH?

Answer 15

• Tensor product wavefunction (SPF combo) and DVR grid gives very poor scaling with system size
• Integrals of MCTDH evolution are over ALL coordinate space (not local like with GWPs)
• MCTDH requires a GLOBAL PES which has complex sum-of-products form