Lecture 1: BOA, coordinate systems Flashcards
• Understand the structure of the time-dependent Schrodinger equation and the challenges associated with its solution o Overview of the time-dependent Schrodinger equation o Derivation of the BOA o Investigation of how choice of coordinates influences the nuclear KE operator (14 cards)
1
Q
- What is the overall goal in time-dependent quantum dynamics?
A
- Experiments capable of measuring timescales and mechanisms of complex dynamical chemical processes (fs-ns range)
- Analysing/interpreting/predicting outcomes of these experiments is difficult as often deal with short lived species in this time scale
- Simulating the dynamics of a reaction would be useful as allows modelling of nuclei/electrons movement, and therefore explain the experiment
2
Q
- Why can classical molecular dynamics not be used for the type of experiments time-dependent quantum dynamics deals with?
A
- Atoms and electrons are quantum objects, which require quantum EOMs so solve accurately
- MD uses a classical model of atoms moving under force (F =ma)
3
Q
- State the time-dependent SEQ, explain its components and how it differs from the time independent SEQ
A
- Left side describes the rate of change of wavefunction at x with time (describes dynamics)
- Hamiltonian operator is a QM operator for the total energy of the system
- X represents position of ALL particles in system (xyz nuc/e-s) described simultaneously
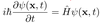
4
Q
- Describe the components of the Hamiltonian operator
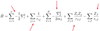
A
5
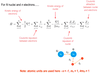
Q
- What approximation is used to simplify the Hamiltonian operator and what is its result
A
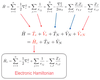
- Born-Oppenheimer approximation separates terms in the Hamiltonian that are related to electrons and nuclei
- Forms the electronic Hamiltonian which can be solved to find electronic states of the system much more simply
- This an be assumed as nuclei move very slow compared to electrons so make little contribution to the overall Hamiltonian.
6
Q
Can the wavefunction we separated similarly to the Hamiltonian operator?
A
- Yes, can be separated in to a part that depends on where electrons are with respect to nuclear position, as well as a nuclear coordinate dependent part

7
Q
Assuming the electronic SEQ is solvable for any set of coordinates R, what form does Hψ take?
A
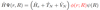
8
Q
- When acted on by the KE operator the new description of the SEQ takes the following form. How does the BOA reduce complexity further and what is the final form taken?

A
- BOA ignores two red terms as when nuclei move, the electronic wavefunction remains fairly constant, so are ignored sa they are very small
- Results SEQ for nuclei moving on a PES given by E(R)
- TN = KE of nuclei
- E(R) is the electronic PES (electronic E calculated at a particular value of coordinates R
- VN(R) = inter-nuclear position
- WE know have a means of describing the nuclei in quantum dynamics
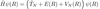
9
Q
- This … … … tells us how nuclear wavefunction changes with the time on a … … …
- From this, interest lies in how ψ describe nuclei and how atoms move according to this equation on a … … … (…) derived from energy of …
A
- This equation of motion tells us how nuclear wavefunction changes with the time on a single electronic state
- From this, interest lies in how ψ describe nuclei and how atoms move according to this equation on the potential energy surface (PES) derived from energy of electrons
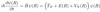
10
Q
How can we solve the TDSE if we know the nuclear eigenstates
A
- If one can figure out the nuclear eigenstates (solutions to TIDSEQ for nuclei) the exact solution of the TDSE at any time can be worked out easily
- Problem of finding next step becomes trivial as exponential is a number that can be calculated.
- If occupying an eigenstate of nuclear Hamiltonian, wavefunction just oscillates in phase
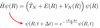
11
Q
- This is a wavefunction propagation of a proton transfer in a double well, how does it relate to the subject matter

A
- Wavefunction propagating by iterative solving of the TDSEQ, and how ψ(R) changes with time, telling us where to go next
12
Q
- What must be considered for a good choice for the coordinates of nuclei, R in evolving system?
A
- Result should lead to mathematically simple nuclear KE operators that are easy to solve
- Correlation/coupling between different DOFs should be minimised (i.e choice of coordinates in 1 direction has little impact on another)
- Ideally matched to problem under investigation (e.g. if interested in a bond dissociation, natural coordinates along/around [angle] should be selected and the ψ along them described
13
Q
Rectilinear coordinate systems lead to simple KE operators that are easy to deal with. Give two examples of types of these coordinates
A
- Cartesian coordinates: x, y, z for each atom
- Mass-weighted normal-mode coordinates: collective normal modes
- Both result in a simple sum of decoupled terms, with no inter-term coupling in KE operator
14
Q
What happens if non-rectilinear coordinates are note used? E.g spherical coordinates
A
- All terms are no longer decoupled, all influence one another and depend on many
- Very hard to press these sorts of operators


