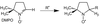Lecture 4 Flashcards
(16 cards)
1
Q
- What is the McConnell equation?
A
- Relates the magnitude of isotropic hyperfine coupling to the amount of spin density on an α-proton
- Used to describe spin polarized systems where an unpaired electron is localised in a p-orbital on a carbon that has no spin density at the nucleus, therefore hyperfine cannot be explained via fermi contact interaction
- Hunds rule says that electrons near this radical will preferentially have the same spin orientation
- This perturbs spin density in C-H sp3 hybrid orbitals, which have s-character localised on hydrogen atoms (hyperconjugation)
- Therefore, it is possible to measure hyperfine due to fermi contact interactions between a radical and a hydrogen atom

2
Q
- What is the largest hyperfine splitting in this molecule?
A
- All dihydrogen environments produce a 1:2:1 splitting pattern except for Hpara (1:1)
- Largest splitting from radical as any unpaired electron leaking on to the ring giving further splitting (consequence of McConnell equation
3
Q
- How does bond polarizability change with bond angle of the hyperfine of an adjacent carbon?
A
- Isotropic β-hyperfine constants explained by (hyperconjugation) overlap of the p-orbital bearing the unpaired electron with the sp3-orbital of the C-H bond at the adjacent carbon
- |a| = Bcos2θ – implies bond is polarised better is parallel and poorer if perpendicular
4
Q
- Originally said … hyperfine originates from unpaired electron localised on … we are … …
- However now know it does not have to be localised there, can be somewhere else and create a net … of … …/… on atom looking at resulting in a …
A
- Originally said isotropic hyperfine originates from unpaired electron localised on atom we are looking at
- However now know it does not have to be localised there, can be somewhere else and create a net excess of spin up/down on atom looking at resulting in a hyperfine
5
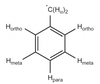
Q
- How is the hyperfine interaction of a p orbital related to the g tensor in the Hamiltonian describing the anisotropic Zeeman interaction?
A
- G tensor is different along all axis, such that varying direction of B0 will give a different resonance along any given position to the next (as seen before)
- In a powder spectrum with axial symmetry the hyperfine interaction (A) can also be anisotropic as electrons in a p orbital will have a stronger hyperfine interaction in the z than xy axis
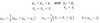
6
Q
- Describe the resulting EPR spectra of the following conditions
- i) aiso << b
- ii) aiso = b
- iii) aiso >> b
A
- i) get regular isotropic spectrum as tensor is just aiso down diagonal (d)
- ii) 0 0 3b on diagonal …?
- iii) 2 lines separated
- intensities depend on how B0 aligns with axis
- c is a pake pattern

7
Q
- To calculate hyperfine interactions, one must average over unpaired electron wavefunction to attain a distribution, what are the resulting values of the tensor in this interaction and why do they take the form they do?
A
- Magnitude of hyperfine along x/y = -b, z = 2b
- Must = 0 overall for anisotropic hyperfine as when tumbling fast, averages to 0 to give isotropic hyperfine.
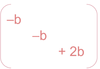
8
Q
- What comprises real world measurements of the hyperfine interaction?
A
- A combination of isotropic and anisotropic components
- Aexp = experimentally observed hyperfine
- Aiso = calculated isotropic (Fermi contact) hyperfine
- b = calculated anisotropic (dipolar) hyperfine

9
Q
- Describe the result of increasing the microwave frequency on the powder spectrum of a system with anisotropic g and hyperfine values
A
- System not tumbling quick enough to average out anisotropy –> get anisotropic interaction
- Changing magnetic field for a given microwave frequency allows interrogation of anisotropy (hyperfine interaction stays constant as is field independent)
- As increase from 1.5 –> 9.75 –> 94 GHz g anisotropy resolved out
- At very low field (plot 1) cant resolve hyperfine as all in middle
- At very high field (plot 3) get three equally spaced lines where anisotropy has resolved. Smallest g value occurs at highest field –> gzz pushed to right
- gxx/yy and Axx/yy somewhere mixed together in spectrum still, must move to higher field to separate similar g values wth identical hyperfine splitting

10
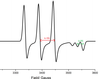
Q
- Determine the spin Hamiltonian parameters from the spectrum, assuming a microwave frequency of 9.25 GHz. Given that a0 = 557G and b0 = 33.35 G for 14N, and assuming b = aiso – AT, calculate the electron spin density on the 14N atom.

A
- I14N = 1, 2I + 1 = 3 lines
- Must be an anisotrpic g tensor and hyperfine splitting from N as 2 sets of lines one of which is the resolved AII (z-axis/principle)
- AT = 55G (measured off plot)
- AII = 20G (measured off plot - accidentally wrote AT)
- aiso = (AT + AT + AII)
- aiso = (55 + 55 + 20)/3
- aiso = 43.33 G
- cs2 = aiso/a0
- cs2 = 43.33/557G = 8%; s character:1
- b = aiso - AT
- cp2 = b/b0
- cp2 = 11.67/33.5 = 35%; p character:4
- indicates large amount of localisation spread across molecule
- orbital hybridisation: λ2= cs2/cp2 = 8/35 = 0.23
11
Q
- What is a major drawback of EPR and what is a solution?
A
- Small number of paramagnetic systems
- Introduce a paramagnetic tracer molecule (e.g. a nitroxide)
12
Q
- Why are nitroxides so stable?
A
- Spin density delocalized favours electronegative O(40 % N, 60% O)
- Full methyl substitution in the β-position also provides steric hindrance as well as removal of structural motif of a β-proton
- This inhibits typical radical reactions like dimerization’s and disproportionation’s
13
Q
- What is a spin label?
A
- Stable radical (often a nitroxide) that can be attached to a non-paramagnetic molecule to probe structure, dynamics and polarity
- E.g. attach a label to all sulphur groups on a specific amino acid in a protein, do ESR
- Looking at dynamics results, degree of rotation speed gives insight into whether the label is inside (hindered) or outside the molecule.
14
Q
- What effect does spin labelling with a nitroxide have on an EPR powder spectrum
A
- Motion of spin probe is strongly influenced by dynamics and local structure of its surroundings.
- EPR is sensitive to rotational diffusion rather than translational
- If the spin probe rotates fast, hyperfine couplings in different directions average to an isotropic value, aiso giving a spectrum of three equal lines
- When rotational motion is prohibited, an anisotropic spectrum forms, indicating something about environment surrounding probe and therefore structure.
15
Q
- What links the tumbling time of a solution to the rotational motion of a spin label and its affect of an EPR powder spectrum?
A
- τc = 1/6DR
- when correlation time low enough, rotational diffusion occurring fast enough so tumbling produces isotropic spectra
- as correlation time slows, anisotropy introduced as rotation of nitroxide hindered in several directions
16
Q
- What is a spin trap?
A
- Solution to trapping specific short -lived radicals and boost detection in EPR
- Produced via chemical reaction (e.g. DMPO – a nitroxide) with molecule trying to trap
- Radical adduct stable for EPR but still short lived
- O is an EWG so depending on what radical is bound, will change in magnitude of Hβ hyperfine splitting.