Lecture 2 Flashcards
(21 cards)
1
Q
- Interaction of the electron spin with the nuclear ‘… …’/’spins’ of atoms gives rise to … … providing the nuclear spin of the atom is non-…
- This arises when an external magnetic moment, B is present that … electron and nuclear magnetic dipoles giving an … hyperfine
A
- Interaction of the electron spin with the nuclear ‘magnetic moments’/’spins’ of atoms gives rise to hyperfine structure providing the nuclear spin of the atom is non-zero
- This arises when an external magnetic moment, B is present that aligns electron and nuclear magnetic dipoles giving an isotropic hyperfine
2
Q
- Describe the isotropic contribution of the hyperfine to the hyperfine energy
A
- Isotropic Hamiltonian relates directly to strength/energy of hyperfine interaction –> Fermi contact interaction
- This includes the wavefuntion, ψ(0), which is the unpaired electron wavefunction at the nucleus
3
Q
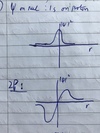
- Using a sketch to aid your answer, describe the wavefunction on a nucleus and the probability of finding an electron in the 1s and 2p orbital. How does this relate to the Fermi contact?
A
- 1s: Finite probability of finding electron at r = 0, would expect hyperfine to be non-zero
- 2p: Probability of finding electron at r = 0 is 0
–> only get fermi contact interaction if unpaired electron is in an s type orbital
4
Q
- In a •CH3 radical, unpaired electron not in an s orbital still produces a hyperfine interaction, why is this?
A
- Electron magnetic field interacts through space with hydrogens producing a dipole-dipole interaction –> Anisotropic interaction; splitting of which depends on orientation of dipoles
- Hyperconjugation also spreads density across molecule ( see McConnell equation – lec 4)
5
Q
- When must the anisotropic term be accounted for in the hyperfine energy?
A
- In high viscosity liquids/ solids where rapid tumbling of radicals is not present, meaning anisotropic hyperfine interaction is non-zero and should be not be ignored
6
Q
- State the Zeeman resonance equation and use it to describe the origin of states in an unpaired electron in a magnetic field
A
- ΔE = hv = gµBB
- An electron has spin = ½ aligned parallel (ms = + 1/2) or anti parallel (ms = - 1/2)
- Interactions of magnetic moment with magnetic field (gµBB*ms) cause energy levels to split as field, B increased
- Radiation absorption matching energy separation causes a transition between the 2 states
7
Q
- Describe two methods of analysing the environment of an unpaired electron via the Zeeman splitting constant
A
- ge = 2.0023, exact value for free electron in vacuum, value differing from this implies electron is interacting with others/in an electric field

8
Q
- Electrons have spin/magnet moment, nuclei surrounding it with their own … …(e.g proton - mI = … ). This contribution is seen by electron as well as the … magnetic field and this contribution scales with …. The electron magnetic moment >> nuclear magnetic moment
A
- Electrons have spin/magnet moment, nuclei surrounding it with their own magnetic field (e.g proton - mI = ± ½). This contribution is seen by electron as well as the applied magnetic field and this contribution scales with distance. The electron magnetic moment >> nuclear magnetic moment
9
Q
- Sketch and label the energy level splitting diagram for a S = ½, I = ½ system, give the overall energy of the interaction as well as the transitions possible between levels
A

10
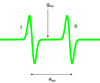
Q
- How does the value of hyperfine splitting relate to the transitions in a S = ½, I = ½ system? specifically the resulting wavepatterns of these transisitons
A
- 1 derivative due to field modulation of peaks to increases sensitivity
- Peaks due to interaction of nucleus and electron give hyperfine splitting, a
11
Q
- What is the electron Zeeman interaction?
A
- When in a magnetic field, B and unpaired electron/radical (S = ½) will split into 2 states
- A low energy state, which is aligned with B: ms = - ½
- A high energy state which is aligned against B: ms = + ½
12
Q
- What is the electron-nuclear hyperfine interaction?
A
- Nuclei of atoms with S ≥ ½ possess a magnetic moment, which produces a local magnetic field at the electron resulting in hyperfine splitting with Zeeman splitting
- E = MsaMI
- From this, info on distribution of the unpaired electron probability density can be attained.
13
Q
- What are the EPR selection rules for transitions between energy levels
A
- Δms = ± 1
- ΔmI = 0
14
Q
- How is the energy change associated with hyperfine transitions in an S = ½ nuclei and I = ½ system related to the magnetic field?
A
15
Q
- Sketch the energy level splitting for a S = ½ and I = ½ system where the nuclear Zeeman splitting is greater than the hyperfine. Include transitions and the hyperfine splitting profile associated with this system
A
- a written before as larger than Zeeman, so interacts first
- N.B. Energy level diagram may be given one way round in terms of splitting then change part way through the question

16
Q
- Sketch the energy level splitting for a S = ½, I = ½, I = ½ system where the hyperfine is greater than the nuclear Zeeman splitting. Include transitions and the hyperfine splitting profile associated with this system
A
Note difference in splitting profile
2 nuclei therfore 2 hyperfine splittings followed by 2 nuclear zeeman splittings

17
Q
- Give the Binomial distribution for n equivalent I = ½ nuclei and I = 1 nuclei
A
- I= ½ (protons), 1 (electron coupled to N)

18
Q
- Sketch the splitting of a •CHCH2 radical
A
- 1 proton environment splits in to 2 with radical electron
- 2 equivalent proton splits cause 1 2 1 splitting when interacting with radical electron
- Get a doublet of triplets
- Larger splitting for environment closer to radical (stronger coupling)

19
Q
- Sketch the splitting of the naphthalene anion radical
A

20
Q
- What is the expected hyperfine splitting from the following molecule?
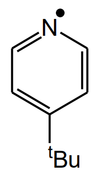
A
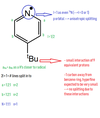
21
Q
- Tips for hyperfine splitting pattern analysis
- Start at edge as … splitting shifts something out to edge
- Use a … to measure distances when reading across spectrum
A
- Tips for hyperfine splitting pattern analysis
- Start at edge as biggest splitting shifts something out to edge
- Use a ruler to measure distances when reading across spectrum


