Lecture 3 Flashcards
(17 cards)
What is interest?
Interest is the opportunity cost of keeping your money as cash under your mattress as opposed to lending. If you borrow money, the interest you have to pay is less than the cost of forgoing the opportunity to have the money in the present.
Main factors driving interest rate movements:
- Monetary policy.
- Expectations of future inflation.
- Bond demand and supply.
- Marginal product of capital (medium- to long-run determinant).
Bond prices and interest rates
Bond prices are sensitive to interest rate movements. They go down when interest rates go up, and vice-versa - negative realtion.
Intuition: Bond prices are the PV of bonds’ cashflows. If interest rates go up, cashflows are discounted more heavily, and the PV falls.
Maturity of bonds and interest rates
The interest rate sensitivity of bond prices increases with maturity
Intuition:
- The cashflows of long term bonds are farther in the future than those of shorter term bonds.
- The PV of far-distant cashflows is more sensitive to the discount rate than the PV of near-term cashflows.
Main tools for measuring and managing interest rate risk
Duration and convexity
Two properties of the performance profile:
- The slope of the performance profile increases with maturity.
- The slope of the performance profile decreases with coupon rate.

Two concepts of duration:
- Macaulay duration (D).
- Modified duration (D∗)
Macaulay duration definition
The weighted average number of years an investor must maintain a position in the bond until the present value of the bond’s cash flows equals the amount paid for the bond. The weight of each cash flow is determined by dividing the present value of the cash flow by the price.
Macaulay duration calculation:
- Find the discount factor for all the periods
- Next, multiply the period’s cash flow by the period number and by its corresponding discount factor to find the present value of the cash flow
- Sum the valued obtained form #2 (numerator)
- Sum of PV Cash Flows (denominator)
- Divide #3 by #4 - A coupon paying bond will always have its duration less than its time to maturity. So, intuitivelly Macaulay duration is the effective maturity of the bond.
Modified duration definition
Modified duration is a formula that expresses the measurable change in the value of a security in response to a change in interest rates. Modified duration follows the concept that interest rates and bond prices move in opposite directions.
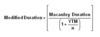
Duration principles:
- As maturity increases, duration increases and the bond becomes more volatile.
- As a bond’s coupon increases, its duration decreases and the bond becomes less volatile.
- As interest rates increase, duration decreases and the bond’s sensitivity to further interest rate increases goes down.
What is the difference between Macaulay duration and modified duration?
The Macaulay duration calculates the weighted average time before a bondholder would receive the bond’s cash flows. Conversely, modified duration measures the price sensitivity of a bond when there is a change in the yield to maturity.
Duration definition
It is a measurement of how long, in years, it takes for the price of a bond to be repaid by its internal cash flows.
Convexity definition
Convexity is a measure of the curvature in the relationship between bond prices and bond yields that demonstrates how the duration of a bond changes as the interest rate changes.
Convexity and risk
As convexity increases, the systemic risk to which the portfolio is exposed increases. As convexity decreases, the exposure to market interest rates decreases and the bond portfolio can be considered hedged. In general, the higher the coupon rate, the lower the convexity (or market risk) of a bond. This is because market rates would have to increase greatly to surpass the coupon on the bond, meaning there is less risk to the investor.
Properties of convexity
If two bonds offer the same duration and yield but one exhibits greater convexity, changes in interest rates will affect each bond differently. A bond with greater convexity is less affected by interest rates than a bond with less convexity. Also, bonds with greater convexity will have a higher price than bonds with a lower convexity, regardless of whether interest rates rise or fall. This relationship is illustrated in the following diagram:

Yield formula



