Lecture 10 Flashcards
European call option
the right, but not the obligation, to buy the underlying asset at a:
- specified price (strike or exercise price)
- specified time (maturity or expiration date).
European put option
the right, but not the obligation, to sell the underlying asset at a:
- specified price
- specified time.
American option
like a European option except it can be exercised at any time prior to maturity.
Notations
Value at maturity of call
Value at maturity of put
Out of the money (OTM
term used to describe a call option with a strike price that is higher than the market price of the underlying asset, or a put option with a strike price that is lower than the market price of the underlying asset. An out of the money option has no intrinsic value, but only possesses extrinsic or time value.
In the money
means that a call option’s strike price is below the market price of the underlying asset or that the strike price of a put option is above the market price of the underlying asset. Being in the money does not mean you will profit, it just means the option is worth exercising. This is because the option costs money to buy.
Net payoff equals:
Payoff at maturity − Cost of establishing position.
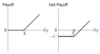
Draw net payoffs of long put, short call, and short put
positions.
How to speculate with options?
- To speculate that the underlying price will go up, we can buy a call.
- Similarly, to speculate that the price of the underlying will go down, we can buy a put.
Speculative strategies
Butterfly spread
a neutral option strategy combining bull and bear spreads. Butterfly spreads use four option contracts with the same expiration but three different strike prices to create a range of prices the strategy can profit from. The trader sells two option contracts at the middle strike price and buys one option contract at a lower strike price and one option contract at a higher strike price. Both puts and calls can be used for a butterfly spread.
Straddle
an options strategy in which the investor holds a position in both a call and put with the same strike price and expiration date, paying both premiums. This strategy allows the investor to make a profit regardless of whether the price of the security goes up or down, assuming the stock price changes somewhat significantly.
Bull spread
an option strategy in which maximum profit is attained if the underlying security rises in price. Either calls or puts can be used. The lower strike price is purchased and the higher strike price is sold. The options have the same expiration date.
The prices of the call and put options are related by:
Absence of arbitrage implies that market value of the replicating portfolio has to be C. We thus have the following equation:
Binomial Option Pricing Model
provides a stream of valuations for a derivative for each node in a span of time, it is useful for valuing derivatives such as American options. It is also much simpler than other pricing models such as the Black-Scholes model.
Risk-neutral probabilities
q and Risk-Neutral Probabilities
Two methods for computing the price of an option — replication vs. RNP
