Lecture 2 Flashcards
(34 cards)
Systems of units
The numerical value of any quantity in a mathematical model is measured with respect to a system of units (for example, meters in a mechanical model, or dollars in a financial model). The units used to measure a quantity are arbitrary, and a change in the system of units (for example, from meters to feet) cannot change the model. A crucial property of a quantitative system of units is that the value of a dimensional quantity may be measured as some multiple of a basic unit. Thus, a change in the system of units leads to a rescaling of the quantities it measures, and the ratio of two quantities with the same units does not depend on the particular choice of the system. The independence of a model from the system of units used to measure the quantities that appear in it therefore corresponds to a scale-invariance of the model.
Scaling

Nondimensionalization

Fluid mechanics

The sress tensor

Viscosity

. The Reynolds number(part 1)

. The Reynolds number(part 2)

The Navier-Stokes equations

Porous medium eqaution

Prolongation of vector fields

Transformations of function

Transformations of the plane
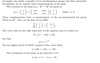
The Lie bracket

Lie groups and Lie algebras

Continuous symmetries of differential equations

Translational invariance

Similarity solution

Scaling invariance

pedestrian derivation

point source solution

The porous medium equation(part 1)

The heat equation

Self-similarity













