Kenneth Harris Flashcards
Discuss how liquid NMR works:
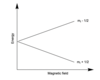
e.g if we have a spin ½ nucleus, and we introduce it into a magnetic field
At 0 magnetic field, both m1 +1/2 and m -1/2 degenerate, however as B increases, energy levels separate. That is why with certain energies we can introduce transitions between these levels.
How is chemical shielding/chemical shift calculated for liquid state NMR and what is it?
Splitting of energy levels is different depending on the environment of the nucleus. For example, a normal carbon atom vs. methane. This is why NMR is useful in chemistry as we can gain information on molecular structure via the difference in energy levels. The exact transition depends on the chemical environment of the nucleus within a molecule.
How can we deduce the change in energy between the levels?
E.g. If we take an isolated nucleus, we can study the energy of the transition of MI=1/2 –> -1/2:
Liquid NMR, Between transitions, how can the frequency of the transition therefore be calculated? Show the equation:
[Hint, it obviously relates to the equation for energy]
Show how the equation for energy differs if we deal with a nucleus sorrounded by electrons (in an atom or molecule) for liquid NMR:
What are 3 parameters of liquid state NMR:
- Chemical shift
- J coupling
- Relaxation time (T1 and T2)
Discuss the significance of relaxation time for liquid state NMR:
For liquids, NMR spectra are very simple because of rapid isotropic tumbling of molecules.
They achieve all orientations of the magnetic field within the time scale of the experiment.
Hence, only the isotropic chemical shift (d) and isotropic J-coupling are observed in the spectrum. The lines observed in the NMR spectrum are usually very narrow due to T2.
Ex. CH3CH2OCH2CH3; 2 proton environments in liquid NMR looks like:
Give an overview of solid-state NMR:
What is the main difference compared to liquid state NMR
What are the consequences of this?
In a solid, the atoms in molecules usually are notmobile, or if they are they have restricted anisotropicmotions. Hence, NMR spectra of solids are notsimplified by rapid isotropic “tumbling”.
Consequence:
- Solid state NMR spectra can depend on several types of NMR interactions in addition to the chemical shift and the J-coupling. The direct dipole-dipole interaction and quadrupolar interactions that actually cancel out to 0.
- In solid state NMR we usually need to consider the full 3D anisotropyof the “NMR interactions”.
Show how the 4 interactions differ in significance for liquid vs. solid state NMR:
For solid state NMR and the significance of the interactions, what do we mean by ‘consider the 3D aniosotropy’?
In general, the NMR spectrum of a single crystal depends on the orientationof the crystal relative to the applied magnetic field:
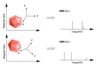
If we move the unit cell and now axis are in different orientation to the applied magnetic field, we measure the spectrum again and the peaks may shift. They move to different positions depending on the orientation of the crystal. There is a reason to why they shift the way they do. The spectrum depends critically on the orientation of the crystal to the applied magnetic field.
Discuss the shape of spectra if a powder is used:
A powder sample has millions of crystal orientations so instead it is a summationof the individual orientations. All possible orientations present. In principle this is very complicated.
We get a peak that typically looks like this. The total line width is very broad.
What are relaxation times?
What is the importance of this for NMR?
T1 – Spin-lattice relaxation time (longitudinal), rate of recovery of longitudinal
T2– Spin-spin relaxation time (transverse), rate of dephasing in x,y plane
For liquid; T1= T2
For solid: T2(10 us-1ms) << T1(1s-1000s)
This means the repetition of a pulse sequence depends on T1. Normally we wait ~ 5*T1. Line width observed is inversely proportional to T2.
So for solid state NMR, the line width is much broader than for liquids. T2 is much shorter for solids and T1 is much longer. Line widths much broader for solid state NMR. Much longer T1 means the recycle delay is much longer.
Discuss the scope of solid-state NMR:
Comparison to X-Ray diffraction (XRD). XRD tells us about the periodic structural properties. Solid state NMR gives us information of the local structureand whether nuclei are nearby. It doesn’t care about periodicity of the environment. Gives us information in the vicinity of the nucleus being studied.
We can study both crystalline and amorphous solids. It is also a useful technique to study dynamics. We can get detailed insights on molecular motion in solids (in contrast XRD gives only a time-averaged representation of the structure).
Discuss in general anisotropic interactions in NMR:
Each of the anisotropic NMR interaction in table 1 is described by a tensor which describes the 3D anisotropy of the interaction. It is related to the coupling of two vectors. The NMR interactions depends on the coupling between two vectors and tensors such coupling mathematically. One vector is I (describing spin-angular momentum of the nucleus being observed) and the other vector depends on the specific interaction (see table 2).
Show the equation that links the hamiltonian for a given type of NMR interaction A:
The tensor described all the information about the NMR interaction and its anisotropy. Details depend on the local structural properties and dynamics of the material containing the nucleus being measured.
What are some properties of vectors (the three components)?
Often different vector properties are linked, such that each component of one vector depends on all threecomponents of the other vector.
Give the definitions for thr trace of the tensor, and axial symmetry
Discuss shielding anisotropy:
Nuclei are shielded from the external field by electrons surrounding the nucleus within a molecule. In a molecule or in a solid, the shielding is anisotropicas the distribution of electrons is usually not spherically symmetrical. The value of the chemical shift depends on the orientation of the molecule relative to the applied magnetic field.
Using the illustration of 13C NMR for HCCl3, discuss exial symmetry and shiedling anisotropy:
This molecule has axialsymmetry, has a 3-fold rotation axis parallel to C-H bond. Would be convenient to choose principal axis system parallel to the rotation axis. Shieling tensor has axial symmetry:
Discuss the relative shilding that occurs at theta = 0, 90 and theta for 13C NMR of HCCl3:
Give the equation for sigma(theta)
Show the independent and dependent parts of this equation and what it symbolises:
What equation does this give rise to?
Show the change in region of peak on solid state spectra for chaninging calues of theta:
(solid-state 13C NMR spectra that would arise from measurements on a single crystal in which there is one type of HCCl3 molecule )
These spectra represent the solid-state 13C NMR spectra that would arise from measurements on a single crystal in which there is one type of HCCl3 molecule in the unit cell. The chemical shift depends on the orientation of the molecule relative to B0.
What differences would occur for a power spectrum compared to the shown single crystal systems:
If we have a powder spectrum, this would be a summation of all spectra of all angles between, but it would also show the probabilities of each orientation. For a powdersample in which allcrystal orientations are equally populated, the observed spectrum is the summationof the individual spectra for each different value of theta. This gives a “CSA powder pattern” where “CSA=chemical shift anisotropy”. It has a characteristic shape.
Discuss intensity distribution of solid state powder NMR and where it arises from?
The intensity distributionis very important. For parallel there can only be two orientations with this angle for B0 (0, 180). As soon as we specify a particular direction, we only are interested in the number of crystals with that angle of . The intensity distribution reflects the fact that, although the crystals in the powder are randomly orientated in space, very few crystals correspond to theta= 0, but many correspond to theta=90.
In the general case, (i.e. not axial symmetry)the principal components of theta are in general not equal: x does not = y which does not = z
Discuss the shape of CSA powder spectra:
What does CSA stand for?
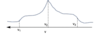
CSA: chemical shift anisotropy
Discuss the different types of direct dipole-dipole interactions and what is happening?
Discuss in more detail the heteronuclear dipole-dipole interaction. What is this called?
Discuss the typical spectran we observe and how we can calculate its frequency/position on the spectrum?
What is the dipolar coupling constant and why is it important for heteronuclear isolated spin pairs?
What is the equation?
What is dipole splitting for heteronuclear spin pairs?
Show for a single crystal containing heteroncuclear isolated spin pair of +1/2 nuclei, what do the spectra look like for theta = 90, 0 and the magic angle?
How would a powder spectra look for a sample containing heteronuclear isolated pair of spin ½ nuclei.?
For a powder sample: need to add up all spectra from all orientations
The NMR spectrum is a summation of the spectra for all crystal orientations (i.e. all values of theta)
Discuss the implications of the 1/r3 term:
What is the implication for homonuclear dipole-dipole interactions with low abundance nuceli?
Why is heteronculear dipole-dipole interaction important for instances where the observed nucleus has another type of NMR active nucleus?
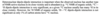
What is quadrupolar interactions?
For a simple distribution of charges, describe quadrupolar interactions and how electropotential can be gained from the electric field gradient:
Draw the quadrupolar interactions between a quadrupolar nucleus with spin 3/2:
What are the different interactions?
Discuss the case of axial symmetry and discuss the perturbation of the zeeman level m1: (don’t need to know the shown equation, we do need the other)
What is the equation?
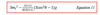
For perturbation of zeeman level equations, what do the energy levels and hence transition frequencies depend on?
Give the equation for the new frequency equation and their dependency on the quadrupole coupling constant:
Discuss the quadrupole interaction for 2H NMR (I=1):
Show the 2H NMR spectrum for a single crystal containing just one type of 2H in the unit ccells: For a specific orientation of theta of the crystal:
The splitting of the lines is given by:
For liquid NMR case, (3cos2*theta-1)=0, and so V = 0, so it doesn’t affect liquid phase. Thus, V depends on the orientation of the crystal .
What values so we get for the quadrupole coupling constant?
Show how the quadrupolar interactions affects powder spectra:
How do quadrupolar and dipole dipole interactions effect liquids?
What are the two general strategies for solid-state NMR:
Discuss pros and cons:
-
Broad line spectra–
* The aim is to study the anisotropic NMR interactions as a source of information on the structural and dynamic properties of solids*
* Analysis: Complicated Information*
* Content: High*
refers to extremely broad spectra achieved from anisotropic spectra
This allows us to study details of broadening due to anisotropic interactions
This gives us detailed information about the solid (geometric structure, dynamics, local interactions etc)
Often the spectra are very complicated, look featureless, unless of type of interaction dominates (e.g. quadrupolar interaction in the case of 2H NMR)
-
High resolution spectra–
* The aim is to average the anisotropic NMR interactions (by experimental techniques such as high-power heteronuclear decoupling and/or magic angle spinning) to generate “isotropic” NMR spectra that resemble the NMR spectra of liquids*
* Analysis: Straightforward Information*
* Content: Low*
aim is to record spectra in such a what that the anisotropic interactions are removed
give liquid like isotropic spectra
simple to interpret
butremoves all information contained in the anisotropic interactions
Discuss the principles of MAS:
Experimental set-up: Powder sample is put in a cylindrical “rotor”, which is spun very rapidly about the cylinder axis, making an angle betawith the B0 field.
Give examples of spectra from MAS domainated by direct-dipole interactions:
Give examples of spectra from MAS domainated CSA:
Discuss high power heteronuclear decoupling:
What are multiple pulse techniques for?
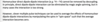
How can dynamics of solids be studied by deuterium NMR?
What are the three dynamic regimes studied when conducting dynamic experiments of solids by 2H NMR?
Discuss single pulse sequences - by using the example of ‘single pulse’ 13C NMR with 1H decoupling:
What are the problems with the single pulse method?
Problems with the ‘single pulse’ method:
13C has low abundance – intensity is intrinsically low
Usually T1(13C) is very long for organic solids – order of minutes. This requires long recycle delays. Typically, we wait 5 * T1. Spectra take a long time to record.
For13C and other low abundance nuclei, in the presence of protons, these two problems are overcome using a technique called “proton to carbon cross polarisation”.
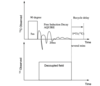
What is 1H—13C Cross polarisation? (CP)
Involves transfer of magnetisation from 1H —13C (remembering 1H are abundant and 13C are dilute). We then observe the 13C NMR signal.
Magnetisation transfer only occurs efficiently ONLY when the Hartman-Hahn condition is established. When maximum 13C magnetisation has developed along the y-axis, acquire the 13C NMR spectrum with proton decoupling.
Magic angle spinning is applied throughout the experiment to give us good resolution and eliminate carbon chemical shift anisotropy.
What are the Advantages of 1H –> 13C CP over 13C single pulse?
What is the disadvantage of 1H –> 13C CP over 13C single pulse:
One significant disadvantage: The 13C magnetisation (My) generated (in figure below) depends on several relaxation processes.
For a given 13C environment, the magnetisation along the y-axis (My) is maximised at a given value of time:
Why do we use high-resolution solid-state 13C NMR?
- Characterizing different polymorphs
- Determining the number of independent molecules in a crystal structure
- Determining the symmetry of the site occupied by a molecule in a crystal
- Detecting disorder in a crystal structure
- Identifying specific intermolecular interactions
- Determining aspects of molecular conformation
The number of peaks observed for a given molecule in high-resolution solid-state 13C NMR depends on the details of the crystal structure (including the symmetry of the crystal structure) and does NOT depend on the symmetry of the isolated molecule
How can we use high resolution-solid state 13C NMR to identify the molecule present in an organic solid:
Solid-state 13C NMR indicates that the molecule exists in the crystal structure as C6 (OH)12
How does high-resolution 13C NMR allow for identification and characterisation of polymorphs:
What is a polymorph?
- p-formyl-trans-cinamic acid
- sodium acetate
- glycine
- m-ABA
Describe how high resolution NMR 13C spectra can determine the number of crytallographic independent molecules in a crystal structure:
- Theory
Definition of “asymmetric unit” : Schematic structure with one molecule (A) in the asymmetric unit. One molecule in one unit gives 6 peaks 1:1:1:1:1:1, but 2 molecules in a unit gives 12 peaks.
Describe howhigh resolution NMR 13C spectra can determine the number of crytallographic independent molecules in a crystal structure:
- Examples:
Describe how high resolution NMR 13C spectra can determine the tautomeric form of a molecule in a crystal structure
Does the m-Aminobenzoic Acid Molecule Exist as the Zwitterion or the Non-Zwitterion in the Five Polymorphs ?
Due to the low X-ray scattering power of hydrogen, the zwitterionic and non-zwitterionic forms may not be readily distinguished by powder XRD
Describe how high resolution NMR 13C spectra can detecting disorder in a crystal structure
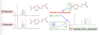
Disorder in the β Polymorph of p-formyl-trans-cinnamic acid
Two Polymorphs: β Polymorph: Crystallization from ethanol g Polymorph: Crystallization from acetone
Discuss how high resolution 13C NMR spectra can deduce disorder in urea inclusion compounds:
Discuss how high resolution 13C NMR spectra can deduce disorder in sodium bromoacetate compounds:
Discuss these graphs
In-situ solid-state NMR studies:
- Solid-state 13C NMR spectra recorded as a function of time during the reaction (not shown here)
- Solid-state 23Na NMR spectra recorded as a function of time during the reaction 23Na NMR: ● Spin I = 3/2 (hence quadrupolar)
● 100% natural abundance
● Dominant anisotropic interaction is the quadrupolar interaction
- Solid-State 23Na NMR Spectra Recorded Using Magic Angle Spinning and High-Power 1H Decoupling
- In-Situ Solid-State 23Na NMR Studies of Reaction in Sodium Bromoacetate
How can we assess hydrogen bonding in cyrstal structures?
Assessing if an OH Group is Engaged in O–H…O Hydrogen Bonding
Prepare the material with deuterated OH group (OD)
Record the solid-state 2H NMR spectrum
The value of the 2H NMR quadrupole coupling constant (c) is sensitive to the O–D…O distance (RD…O) in a hydrogen bond:
Discuss features of solid-state 2H NMR
What is the dominant interaction?
What does a typical spectrum look like and what does the splitting depend on for axial symmetry? What is the equation for this?
2H is a quadrupolar nucleus (spin I = 1)
The dominant anisotropic interaction in solid-state 2H NMR is the quadrupolar interaction
Quadrupolar Interaction (for spin I ≥ 1):
The interaction between the electric quadrupole moment of the nucleus and the electric field gradient at the nucleus
In solution: quadrupolar interaction is averaged to ZERO
In solid: quadrupolar interaction depends on the orientation of the crystal with respect to Bo
For a given 2H environment in a crystal, the 2H NMR spectrum comprises two lines The splitting depends on the orientation qof the crystal relative to the applied magnetic field (Bo )
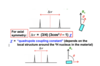
How does the appearance of the axial graph change when a single crysal measured at different orientations is used for 2H NMR? and for powder sample?
How can molecular motion be studied by solid state 2H NMR?
The shape of the 2H NMR “powder pattern” is very sensitive to the rate and mechanism (geometry) of molecular motion, especially for motions with rates in the range 103 – 107 s –1
Exam question: Hydrogen-bond dynamics of polymorphs of L-Glutamic Acid
What are the dynamic properties of the ammonium group?
Solid-state 2H NMR spectroscopy for polymorphs of L-glutamic acid deuterated in the –ND3+ group
Calculate the activation energy of the polymorphs:
You need to plot a graph of ln(k) vs. 1000 x T, the gradient = -Ea/R?
Discuss how the dynamics of ammonium can be studied:
Structure determination from powder X-ray diffraction gives the positions of non-hydrogen atoms, but cannot reliably distinguish the orientation of the NH4 + cation
What are the general techniques used to investigate dynamics?
Discuss the dynamics of urea inclusion compounds:
Which anisotropic interactions are important in each of the following cases? *POPULAR
Note: (C6H5)3P=O denotes a sample with natural isotopic abundances
(C6D5)3P=Odenotes a 99% deuterated sample.
Solid state 31P NMR of (C6H5)3P=O
Solid state 13C NMR of (C6H5)3P=O
Solid state 1H NMR of (C6H5)3P=O
Solid state 2H NMR of (C6D5)3P=O (1% 1H!!)
Solid state 1H NMR of (C6D5)3P=O (1% 1H!!)
Natural Abundance:
1H ½;high abundance (99.8%), 2H 1; low abundance (0.02%), 13C ½; low (0.1%), 14N 1, (high 99%) 15N ½; low (0.4%), 19F½ (100%), 27Al 5/2 (100%), 29Si½ (4.7%), 31P½ (100%), 17O 5/2 (0.04%)
If there is an abundant nucleus, there is a high chance of dipole-dipole interaction.
For this type of question, you need to consider both the properties of the nucleus being “measured” and the properties of the nuclei in the close vicinity of the nucleus being “measured”. Then, recall the following points discussed in the lectures:
Chemical shielding anisotropy: In general, all nuclei will exhibit chemical shielding anisotropy in solids (except in certain special cases, such as the nucleus being on a site of cubic symmetry or the nucleus being in a molecule that undergoes isotropic reorientational motion).
Direct dipole-dipole interaction: If the nucleus being “measured” has other NMR-active nuclei in its close vicinity, then direct dipole-dipole interaction will be observed (recall that the direct dipole-dipole interaction decreases significantly as internuclear distance increases, so it is appreciable only for nuclei that are close to each other). If the NMRactive isotopes of the elements in close vicinity have only low abundance (e.g. 13C in the case of samples with natural isotopic abundance), then they can be ignored in the context of direct dipole-dipole interaction. Recall that the direct dipole-dipole interaction can be both homonuclear (i.e. between nuclei of the same type) and heteronuclear (i.e. between nuclei of different types).
Indirect dipole-dipole interaction (J-coupling): As discussed in lectures, the indirect dipoledipole interaction is usually insignificant in comparison to direct dipole-dipole interaction and can be neglected.
Quadrupolar interaction: If the nucleus being “measured” has I ≥ 1, then there is quadrupolar interaction (and it is often the dominant anisotropic interaction, as in the case of 2H NMR). If the nucleus being “measured” has I = ½, there is no quadrupolar interaction.
solid-state 31P NMR of triphenylphosphine oxide (C6H5)3P=O
Measure 31P NMR (recall that 31P has I = ½) Of the other nuclei present, only 1H is abundant and NMR-active (the abundant isotopes for C and O are 12C and 16O, which are not NMR-active)
Hence, the significant anisotropic interactions are: 31P chemical shift anisotropy 31P…1H direct dipole-dipole interaction 31P…31P direct dipole-dipole interaction [however, this interaction is probably not very significant in this case as nearest neighbour 31P nuclei are far apart (they are in different molecules)]
Note 1: as 31P has I = ½, there is no quadrupolar interaction
Note 2: as discussed in lectures, the 31P…1H indirect dipole-dipole interaction (J-coupling) may be neglected as it is negligible in comparison to the 31P…1H direct dipole-dipole interaction
solid-state 13C NMR of triphenylphosphine oxide (C6H5)3P=O
Measure 13C NMR (recall that 13C has I = ½) Of the other nuclei present, both 31P and 1H are abundant and NMR-active
Hence, the significant anisotropic interactions are: 13C chemical shift anisotropy 13C…31P direct dipole-dipole interaction 13C…1H direct dipole-dipole interaction
Note 1: as 13C has I = ½, there is no quadrupolar interaction
Note 2: 13C…13C direct dipole-dipole interaction can be neglected because of the very low abundance of 13C, which means that a given 13C nucleus is very unlikely to have another 13C nucleus in its close vicinity
solid-state 1H NMR of triphenylphosphine oxide (C6H5)3P=O
Measure 1H NMR (recall that 1H has I = ½) Of the other nuclei present, 31P and 1H are abundant and NMR-active
Hence, the significant anisotropic interactions are: 1H chemical shift anisotropy 1H…31P direct dipole-dipole interaction 1H…1H direct dipole-dipole interaction
Note 1: as 1H has I = ½, there is no quadrupolar interaction
Note 2: in this case, the 1H…1H direct dipole-dipole interaction will be the dominant anisotropic interaction, because 1H has a very large value of magnetogyric ratio and because each 1H nucleus has many other 1H nuclei in its close vicinity (recall the equation given in lectures for the dipolar coupling constant)
solid-state 2H NMR of triphenylphosphine oxide (C6D5)3P=O
Measure 2H NMR (recall that 2H has I = 1 and is therefore a quadrupolar nucleus)
As discussed in lectures, the quadrupolar interaction dominates all other anisotropic interactions in the case of 2H NMR
solid-state 1H NMR of triphenylphosphine oxide (C6D5)3P=O
As the material is 99% deuterated, 1H becomes a “dilute” nucleus in this case and 2H is abundant. Of the other nuclei present, both 31P and 2H are abundant and NMR-active.
Hence, the significant anisotropic interactions are: 1H chemical shift anisotropy 1H…31P direct dipole-dipole interaction 1H…2H direct dipole-dipole interaction (although this interaction is generally weak and can probably be ignored)
Note 1: 1H…1H direct dipole-dipole interaction can be neglected in this case because only 1% of the H is present as 1H, which means that a given 1H nucleus is very unlikely to have another 1H nucleus in its close vicinity
Exam question: A tri-substituted phosphine oxide O=PR3(with three identical substituents R) can form two crystalline polymorphs. In the crystal structure of each polymorph, there is one crystallographically independent O=PR3molecule. In polymorph A, the P=O bond lies along a crystallographic 3-fold symmetry axis, whereas in polymorph B, the molecule does not reside on a crystallographic symmetry site. The solid-state 31P NMR spectra recorded (with high-power 1H decoupling but with no magic-angle spinning) for powder samples of the two polymorphs are shown below.
Exam question:
A tri-substituted phosphine oxide O=PR3(with three identical substituents R) can form two crystalline polymorphs. In the crystal structure of each polymorph, there is one crystallographically independent O=PR3molecule. In polymorph A, the P=O bond lies along a crystallographic 3-fold symmetry axis, whereas in polymorph B, the molecule does not reside on a crystallographic symmetry site. The solid-state 31P NMR spectra recorded (with high-power 1H decoupling but with no magic-angle spinning) for powder samples of the two polymorphs are shown below.
For each polymorph, determine the principle values of the 31P chemical shift anisotropy tensor and hence determine the isotropic 31P chemical shift in each case.
Exam question:
The following molecule is prepared with the two phenyl rings fully deuterated but with all other sites at natural isotopic abundances.
Exam question:
Assuming that the solid expands as temperature is increased, how will the solid-state 1H NMR spectrum for the powder sample change with increasing temperature?
Exam question:
(c) Describe the appearance of the solid-state 1H NMR spectrum for a powder sample in each of the following cases:
(i) the guest molecules are as shown above, but the host structure contains perhydrotriphenylene molecules with natural isotopic abundances (C18H30).
Exam question
(ii) the hydrogen sites in the C≡C–H groups of the guest molecules shown above are 98% deuterated, and the host structure contains fully deuterated perhydrotriphenylene molecules (C18D30).
Exam question:
EXAM QUESTION:
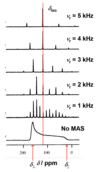
Solid-state 13C NMR spectra for solid dicyclopentadienyl zirconium dichloride are shown in Figure 1. In all cases, the spectra were recorded with high-power 1H decoupling. The spectrum at the bottom was recorded without magic-angle spinning (MAS), whereas the other spectra were recorded at different MAS frequencies (denoted Vr).
(a) From the spectra recorded with MAS, deduce how many isotropic 13C resonances are observed, and in each case determine the isotropic 13C chemical shift.
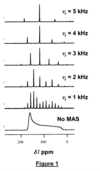
As shown in the annotated figure below, only one peak (at = 118 ppm) doesn’t move when the MAS frequency is changed, so this peak is the only isotropic 13C resonance in this case.
EXAM QUESTION
Solid-state 13C NMR spectra for solid dicyclopentadienyl zirconium dichloride are shown in Figure 1. In all cases, the spectra were recorded with high-power 1H decoupling. The spectrum at the bottom was recorded without magic-angle spinning (MAS), whereas the other spectra were recorded at different MAS frequencies (denoted Vr).
From the spectrum recorded with no MAS, estimate the principal components of the13C chemical shift anisotropy tensor and hence determine the trace of the tensor. Comment on the relation between the trace of the 13C chemical shift tensor and the information derived in part (a).
EXAM QUESTION:
Figure 2 shows experimental 2H NMR spectra recorded at four different temperatures for deuterated L-serine (left side) and simulated 2H NMR spectra (right side) calculated for a proposed dynamic model for several different rates of motion (denoted k). From these data, determine the activation energy for the dynamic process.
EXAM QUESTION:
A crystalline material contains a diol molecule in which the two OH groups are in crystallographically distinct environments and undergo dynamic processes at different rates. Experimental solid-state 2H NMR spectra recorded at four different temperatures for a powder sample of the deuterated material (containing two OD groups) are shown in Figure 3, together with a set of simulated 2H NMR spectra, calculated for a proposed dynamic model in which the rates of the dynamic processes for the two OD groups are denoted k1 and k2. By drawing appropriate graphs, determine the activation energies for the dynamic processes involving the two OD groups.
EXAM QUESTION:
A metal-organic framework material is prepared with a low loading of molecular hydrogen (H2) included as guest molecules inside the framework. The framework does not contain any abundant NMR-active isotopes, and the hydrogen molecules are at natural isotopic abundance. The 1H NMR spectrum is recorded (with no magic-angle spinning) for a powder sample of this material at 110 K. Assuming that the hydrogen molecules do not undergo any reorientational motion at this temperature, sketch the 1H NMR spectrum.
EXAM QUESTION:
Solid-state 13C NMR spectra for a powder sample of a crystalline organic material are shown on the next page, recorded with magic-angle spinning (MAS) and high-power 1H decoupling. The MAS frequency is denoted r. When the solid is dissolved in an appropriate solvent, the liquid-state 13C NMR spectrum of the resulting solution contains one 13C resonance at δ = 32 ppm and one 13C resonance at δ = 168 ppm.
(a) Determine the number of isotropic 13C resonances in the solid-state 13C NMR spectrum of this material. For each isotropic 13C resonance, determine the value of the isotropic 13C chemical shift.
In order to explain your reasoning, an annotated copy of the spectra shown on the next page should be included within your answer.
Exam question: Deduce (giving an explanation of your reasoning) how many molecules are present in the asymmetric unit of the crystal structure.
Exam question:
Exam question:
Exam question:
Question 3
The solid-state 13C NMR spectrum for a powder sample of a crystalline organic material (with natural isotopic abundances) is shown below, recorded with high-power 1H decoupling but without magic-angle spinning. From X-ray diffraction studies, it is known that there are two distinct carbon environments in the crystal structure.
(a) Determine the principal values of the 13C chemical shift anisotropy tensor for each13C site in the crystal structure, and hence determine the isotropic 13C chemical shift for each 13C site. Comment on the local symmetry of the two 13C sites in the crystal structure.
Exam question:
(b) Sketch the solid-state 13C NMR spectrum for the same powder sample recorded under conditions of high-power 1H decoupling and very rapid (e.g. r > 50 kHz) magic-angle spinning.
