Introduction into Biomechanics tutorial

Question 1

In the figure above, given that the distance from the axis of rotation of the knee to the ankle is 0.45 m, calculate the moment produced by an ankle weight (100N) when the leg is: HORIZONTAL

Answer 1

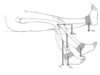
Moment = Fd = 100 N x 0.45 m = 45 Nm

Question 2

In the figure above, given that the distance from the axis of rotation of the knee to the ankle is 0.45 m, calculate the moment produced by an ankle weight (100N) when the leg is: VERTICAL

Answer 2

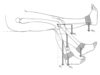
Fd = 100 N x 0 m = zero Nm

Question 3

In the figure above, given that the distance from the axis of rotation of the knee to the ankle is 0.45 m, calculate the moment produced by an ankle weight (100N) when the leg is: 30^o to the horizontal

Answer 3

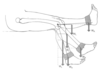
iFd = 100 N x (Cos30o x 0.45 m) = 38.9 Nm (COS = A/H using Pythagorean trigonometric identity)

Question 4

In the figure above, given that the distance from the axis of rotation of the knee to the ankle is 0.45 m, calculate the moment produced by an ankle weight (100N) when the leg is: 30o to the vertical

Answer 4

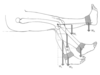
Fd = 100N x (COS60o x 0.45 m) = 22.5 Nm

Question 5

In the figure above, given that the distance from the axis of rotation of the knee to the ankle is 0.45 m, calculate the moment produced by an ankle weight (100N) when the leg is: Why would the actual moment be greater than your calculated figure?

Answer 5

We did not consider the weight of the leg and foot. These provide additional flexion moments.

Question 6

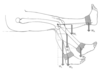
Describe the knee extensor muscle moment required through the range of knee movement in the free weight knee extensor exercise illustrated.

Answer 6

It would be maximal in the fully extended knee position, falling slowly to start with as the angle to the horizontal increases form zero…..The moment required to balance the clockwise torque drops more quickly in the latter half of flexion, and is zero at 90 degrees of flexion (This assumes that patellar tendon has a constant extensor moment arm throughout this range).

Question 7

In the figure above, the mass of the body above the knees is 50 kg. If the length of the leg is 0.45 m, calculate the knee flexor moment produced by upper body weight when the leg is: VERTICAL

Answer 7

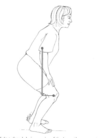
Zero, as the weight of upper body passes through the knee joint = no moment arm

Question 8

In the figure above, the mass of the body above the knees is 50 kg. If the length of the leg is 0.45 m, calculate the knee flexor moment produced by upper body weight when the leg is: 30o from vertical:

Answer 8

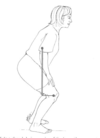
SIN30o x 0.45 m x (9.81 m.s-2 x 50 kg) = 110.4 Nm

Question 9

In the figure above, the mass of the body above the knees is 50 kg. If the length of the leg is 0.45 m, calculate the knee flexor moment produced by upper body weight when the leg is: 45o from vertical

Answer 9

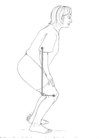
SIN45o, etc. = 156.1 Nm

Question 10

In the figure above, the mass of the body above the knees is 50 kg. If the length of the leg is 0.45 m, calculate the knee flexor moment produced by upper body weight when the leg is: 60o from vertical

Answer 10

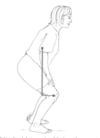
SIN60o etc. = 191.2 Nm

Question 11

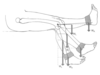
Discuss the knee extensor muscle moment required through the range of knee movement in the closed chain knee extensor exercise illustrated. Compare this with the free weight (open chain) and discuss the functional / clinical implications of this knowledge.

Answer 11

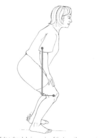
Extensor moment is largest at high angles of flexion as opposed to the other mode of loading, also of higher magnitude. Differences can be tailored to clients condition.