Hypothesis testing for two means (independent samples, equal variances)

Question 1

what features does two samples have?

Answer 1

two samples are unrelated and drawn randomly from a different populations (independent)

eg. men and women, left and right handed people

samples are linked in some way (dependent/paired) mix up order and checking if it makes sense (before and after weights)

eg. two questions are asked of the same person,

Question 2

independent- population standard deviations are known

1. Hypothesis

2. Test Statistic
3. Decision Test
4. Conclusion

Answer 2

—H₀: μ₁= μ₂
—H_A: μ₁≠ μ₂

Question 3

independent- population standard deviations are known

1. Hypothesis
2. Test Statistic
3. Decision Test

4. Conclusion

Answer 3

—in terms of whether sufficient evidence to reject null hypothesis.

Question 4

independent- population standard deviations are known

1. Hypothesis
2. Test Statistic

3. Decision Test

4. Conclusion

Answer 4

—Compare to a standard normal distribution for decision rule.

Question 5

independent- population standard deviations are known

1. Hypothesis

2. Test Statistic

3. Decision Test
4. Conclusion

Answer 5

Question 6

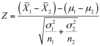
How to determine the confidence interval for two samples that are independent and their population standard deviations are known

Answer 6

100(1-α)% Confidence interval

Question 7

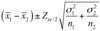
what is the problem with the previous formulas for two indepedent samples where the population standard deviation is known?

Answer 7

—Population variances are almost always unknown
—Usually we have to estimate the population variance using the sample variance

Question 8

<!--StartFragment-->

Independent – population standard deviations unknown<!--EndFragment-->

what does the test depend on?

Answer 8

—Test to use depends on whether the population variances of the two different populations can be assumed to be equal or not.
—If variances are equal, test can be performed by hand
—If variances are not equal, test is complicated – we will rely on software (Minitab)

Question 9

how to test if the two samples have equal population variances?

1.Hypotheses

2. Test Statistic
3. Decision Rule
4. Conclusion

Answer 9

H₀: σ₁²=σ₂² - that is, both populations have the same variance

H_A: σ₁²≠σ₂² - that is, the variances of the populations are different

—Alternative is (almost) always “≠”

Question 10

how to test if the two samples have equal population variances?

1. Hypotheses
2. Test Statistic
   * *3.Decision Rule**
3. Conclusion

Answer 10

Compare to an F distribution with numerator df = n₁-1; denominator df=n₂-1 (see Table 5 in text, pages 559-562)

—F-distribution: Requires two degrees of freedom
—Tables give upper cut-off point for α=0.05/0.025/0.01/0.005
— two-sided test; look up table for α/2
—E.g. for α=0.05, need to look up tables for α=0.025

Question 11

how to test if the two samples have equal population variances?

1. Hypotheses
   * *2.Test Statistic**
2. Decision Rule
3. Conclusion

Answer 11

—General rule – put larger sample variance on top
—This makes it easier to use the F tables

Question 12

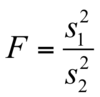
how to test if the two samples have equal population variances?

1. Hypotheses
2. Test Statistic
3. Decision Rule
   * *4.Conclusion**

Answer 12

EITHER
—There is insufficient evidence to reject the null hypothesis, and we can assume the population variances are equal.
—OR
—There is sufficient evidence to reject the null hypothesis. We cannot assume the population variances are equal.

Question 13

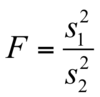
<!--StartFragment-->

If the two population variances are equal, we can test for equality <!--EndFragment-->

_1. Hypotheses _

2. Test Statisic
3. Decision Rule
4. Conclusion

Answer 13

—H₀: μ₁= μ₂
—H_A: μ₁≠μ₂

Question 14

<!--StartFragment-->

If the two population variances are equal, we can test for equality <!--EndFragment-->

1. Hypotheses

2. Test Statisic : why pool the sample variances?

3. Decision Rule
4. Conclusion

Answer 14

—If both populations have the same variance, then each sample is providing a different estimate of the same thing.
—So, rather than choose one variance to use, we use a weighted average of both sample variances to estimate the (common) population variance.
—Weighting is done according to sample size.

Question 15

If the two population variances are equal, we can test for equality

1. Hypotheses

2. Test Statisic

3. Decision Rule
4. Conclusion

Answer 15

Question 16

<!--StartFragment-->

If the two population variances are equal, we can test for equality <!--EndFragment-->

1. Hypotheses
2. Test Statisic

3. Decision Rule

4. Conclusion

Answer 16

—Decision Rule: Compare to a t-distribution with n1+n2-2 df (same as denominator in pooled variance formula)
—
—Conclusion: In terms of whether evidence is sufficient to reject null hypothesis.

Question 17

<!--StartFragment-->

If the two population variances are equal, we can test for equality <!--EndFragment-->

1. Hypotheses

2. Test Statisic: what is the purpose of a pooled variance?

3. Decision Rule
4. Conclusion

Answer 17

—Test statistic uses pooled variance to estimate standard error of the difference between the means

Question 18

<!--StartFragment-->

If the two population variances are equal, we can test for equality <!--EndFragment-->

1. Hypotheses

2. Test Statisic: what often happens to population mean?

3. Decision Rule
4. Conclusion

Answer 18

In general, if testing for equality of means, then μ1= μ2, so the μ1- μ2 term drops out (=0)

Question 19

<!--StartFragment-->

Confidence interval for difference between two means

what do we have to assume?

Answer 19

– independent data, population variances assumed equal

Question 20

Confidence interval for difference between two means – independent data, population variances assumed equal

Answer 20

Question 21

<!--StartFragment-->

What if variances aren’t equal for different between two means?

Answer 21

—Minitab (or other software packages) will compute a p-value (for hypothesis test), or a Confidence Interval (if required).

Question 22

<!--StartFragment-->

How about paired samples?<!--EndFragment-->

Answer 22

—i.e. have two samples, X₁ and X₂, which are paired.
—For each observation, calculate X_d=X₁-X₂.
—Then calculate X̄_d and s_d (mean and standard deviation of differences).

Question 23

Conduct Hypothesis test on paired samples

1. Hypotheses

2. Test Statistic
3. Decision Test
4. Conclusion

Answer 23

—H₀: μ_d=0
—H_A: μ_d≠0

Question 24

Conduct Hypothesis test on paired samples

1. Hypotheses

2. Test Statistic

3. Decision Test
4. Conclusion

Answer 24

2. Test Statistic

Question 25

Conduct Hypothesis test on paired samples

1. Hypotheses
2. Test Statistic

3. Decision Test

4. Conclusion

Answer 25

3. Decision Test

: Compare to a t-distribution with n_d-1 df.

Question 26

Confidence interval for the difference between two means, paired data

Answer 26

Question 27

What about testing two proportions?

Answer 27

—Our samples must be independent!
Use the idea that sample proportion is normally distributed, samples independent, then

Question 28

Testing Two proportions

1. Hypotheses
2. Test Statistic

3. Decision Rule

4. Conclusion

Answer 28

—We compare this to a Z~N(0,1) distribution for the decision rule.

Question 29

Testing Two proportions

1. Hypotheses

2. Test Statistic

3. Decision Test
4. Conclusion

Answer 29

Question 30

Testing Two proportions

1. Hypotheses

2. Test Statistic
3. Decision Test
4. Conclusion

Answer 30

—If the null hypothesis is true, both the sample proportions are estimating the same thing.
—So, to find a standard error, we use a pooled sample proportion.

Question 31

when may you use the pooled-variance t-test?

Answer 31

to determine whether there is a significant differnt between the means of two populations

(if population is not normally distributed, the pooled variance t test can still be used if sample sizes are large enough, typically greater than 30)

Question 32

when should you use F test?

Answer 32

onl when each of the two populations are normally distributed. F test is very sensitive to normality assumption