GRE Math Flashcards
Adjacent Squares (Addition)
Slope
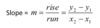
Point-Slope Form
Slope-Intercept Form
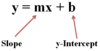
When to use estimation?
Multiple choice answers when answers are far apart
Adjacent Squares (Subtraction)
Squares of 5
- Number to be squared: 752
- Remove the 5: 75 -> 7
- Add one to the remaining digit: 7 -> 8
- Multiply the two: 7 * 8 = 56
- Put this in front of 25: 752 = 5625
Dividing by 5
- Double a number then divide by 10
- Divide by 10 then double
Doubling & Halving
- Dividing and multiplying factors by 2 to get easier factors
- You can do this multiple times
- Example
- Suppose 16 * 35
- 16 / 2 = 8
- 35 * 2 = 70
- 70 * 8 = 560
- Suppose 16 * 35
Squaring Multiples of 10
- Square the 10, square the non-10 and multiply the two
- Example: 402 = 42 * 102 = 16 * 100 = 1600
When to use doubling and halving with 5
- A factor ends in 5 (45)
- A factor is an odd multiple of 50 (150)
4 Random Number Game
- Take 4 random numbers in 0-9
- Use all of the numbers to find all numbers in 1 - 20
GRE Quantitative Question Types
- Multiple Choice
- Multiple Answer
- Number Entry
- Quantitative Comparison
Quantitative Comparison Answers
A) Quantity A is always better
B) Quantity B is always better
C) Both are always equal
D) Cannot be determined
QC Approximations
- Use estimation
- Compare parts instead of the whole
- If both columns have only numbers then D can’t be the answer
- Example
- Q(A) 32.8% of 5,929 Q(B) 41.6% of 5,041
- 33.3-% of 6000- = 2000-
- 40+% of 5000+ = 2000+
- Therefore (B)
- Q(A) 32.8% of 5,929 Q(B) 41.6% of 5,041
QC Matching Operations
- Equalities: >, <, =
- Allowable Operations
- Add to both sides
- Subtract from both sides
- Multiply or divide the same positive number
Rounding
- 0 - 4 = Round Down
- 5 - 9 = Round Up
- Only look one place to the right when rounding
- *10.49999 = 10
Quantity Increase (Percentage)
x = Q * (1 + (P% as a decimal))
x = 230 * (1 + 0.4)
x = 230 * 1.4
x = 322
Quantity Decrease (Percentage)
x = Q * (1 - (P% as a decimal))
x = 80 * (1 - 0.7)
x = 80 * (0.3)
x = 24
Find the Multiplier
Distributive Property
Multiplication distributes over addition and subtraction
Works if addition/subtraction is in the numerator, but NOT the denominator
Percent Increase Equation
Amount * (1 + Percent Decimal)
$425 increases by 30%
$425* (1 + 0.3) = $425 * 1.3 = $552.5
Percent Decrease Equation
Amount * (1 - Pecent Decimal)
$700 decreases by 25%
$700 * (1 - 0.25) = $700 * 0.75 = $525
Simple Interest
- Each payment is paid against the original principal amount.
- Not the way interest works, but is good for illustrating the general idea and estimation.
- Amount = Principle + (Principle * Percent * Repetition)
- A = P + (P*D*R)
- Example: Bob deposits $1000 in an account that yields 5% simple interest annually.
- 5% of $1000 = $50
- 1 year: $1000 + $50 = $1050.00
- 2 years: $1050 + $50 = $1100.00
- 3 years: $1100 + $50 = $1150.00
- Etc…
Compound Interest
- Interest percentage paid according to the current total, not the original principal, essentially stacking the amount.
- Example: Bob deposits $1000 in an account that yields 5% compound interest annually.
- Start = $1000
- 1 year = 1000*(1.05) = 1050
- 2 year = 1050*(1.05) = 1102.5
- 3 year = 1102.5*(1.05) = 1157.625
- Etc.
Compound Interest Formula (Simple)
In y years, the principal will be multiplied by the percent increase multiplier y times. Let P be the principal and r be the multiplier. The total amount in the account after y years is given by:
Compound Interest Multiplier
Compound Interest Formula (Full)
Inverse of a Fraction
You can always take the inverse of a numerical or variable fraction.
Cross Multiply Fractional Equalities
Fractional equalities can always be cross-multiplied
Multiply to get Equalities
Multiply both sides to get equalities with other equations
3w = 2x
15w = 8y
5*3w = 5*2x
15w = 10x
Therefore 10x = 8y
Ratio
- a fraction that compares part-to-whole or part-to-part
- 6:13 = 6 for every 13
P to Q Form (Ratios)
“The ratio of boys to girls is 3 to 4”
Fraction Form (Ratios)
“The ratio of boys to girls is 3/4”
*This is the most useful form for problem solving
Colon Form (Ratios)
“The ratio of boys to girls is 3:4”
Idiom Form (Ratios)
“For every 3 boys, there are 4 girls”
How do we solve the majority of ratio problems on the test?
- set two equivalent fractions equal
- this is an equation of the form: fraction = fraction
- this is called as a proportion
- 7/10 = 49/70
Proportion
- two fractions that are equal
- fraction = fraction
- Example: In a class, the ratio of boys to girls is 5:8. If ther are 40 girls, how many boys are there?
Scale Factor
- a number which scales or multiplies a given quantity
- Ex: In a class, the ratio of boys to girls is 3:7. If there are 32 more girls than boys, how many boys are there?
- 3n - 7n = 4n
- 4n = 32
- n = 8
- 3n = 3*8 -> n = 24
Portioning
- adding the two ratio numbers together to get the full number that each factor is a part of
- Ex: Boys to girls is 3:5. Boys are what fraction of the whole?
- 3+5 = 8
- Boys are 3/8 of the whole
How do you solve a proportion?
- cross-multiply then divide by the known number
Absolute Quantity (Fractions)
- when an actual number is present for a fractional amount you can find other absolute quantities of related fractions
Least Common Multiple (Ratios)
- use the LCM to relate ratios and solve problems
- B:C = 3:4 & C:S = 7:11
- LCM of 7 and 4 = 28
- B:C = 3*7:4*7 = 21:28
- C:S = 7*4:11*4 = 28:44
- B:C:S = 21:28:44
What does “x percent of” a number or fraction mean?
x over 100 times the number or fraction
Compound Interest (Quarterly)
