Graphs-Book Notes Flashcards
(19 cards)
Adjacency Matrix Time?
Defn?
Sparse or Dense?
Edge Check O(1)
Space O(n^2)
Represents graph in n x n matrix, whose (i,j) entry is 1 - if there is an edge, 0 - otherwise.
Undirected graphs, the matrix is symmetric (as it can be traversed in either direction) Used on dense graph
Adjacency List Time?
Defn?
Sparse or Dense?
Checking for edge: O(|E| + |V|)
Space: O(E)
Consists of linked list of vertices, each vertex has a list of the vertices which u has an outgoing edge.
Used on sparse graph
Depth First Search
Time?
Algo?
Time: O(|E| + |V|) Linear Time
dfs (G):
NOTE: This top level handles the disconnected graph base by making sure to kick off a new explore to traverse any vertex not covered by the recursion below.
for all v in V
visited(v) = false
for all v in V
if not visited(v)
explore(v)
explore(G,V)
Input G = (V, E) is a graph;
Output: visited u is true for all nodes u reachable from v
visited(v) = true
previsit(v)
for each edge (v,u) in E:
if not visited (u)
explore(u)
postvisit(v)
A graph is connected if?
There is a path between any pair of vertices.
What a connected components?
A subgraph that that every vertex is connected internally, but has no edges that connect out to the remaining vertices.
What are pre and post visit for
Algo?
Defn?
Uses?
previsit(v)
pre[v] = clock
clock = clock + 1
postvisit(v)
post[v] = clock
clock = clock + 1
Previsit keeps track of when a node is first discovered in the tree, post visit is the time when all of it’s child nodes have finished being discovered.
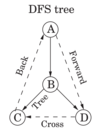
Types of edges in DFS for Directed Graph
Tree Edge
Forward Edge
Back Edge
Cross Edge
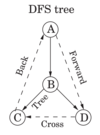
Tree - Main edges that are part of forest (traversal)
Forward edges - edges that lead from a node to a non child descendant
Back Edges - edges that lead to an ancestor
Cross Edges - not a descendant or ancestor, lead to peer that was already explored.
———————– (Probably not needed)
Can be determined by pre/post number.
Tree/Forward U[V[]V ]U
Back V[U[]U ]V
Cross: V[]V U[]U
Cycle/Acyclic
How and Time To discover?
A Cycle can be discovered with a depth first search in linear time if it encoutnerd a back edge.
What is a topological sort of a graph (linearize)
Time?
How is it done?
Time: Linear
A topological sort of a graph allows it to be ordered in a way that each edge goes from an earlier vertex to a later one. (E.g.) Gives order of precidence so that constraints (pre conditions) of a vertex are all satistfied.
Perform tasks in decreating order of their post number.
Sink: Node with smallest post order
Source: Node with highest post order.
Strongly Connected Components
Two nodes u and v in a directed graph are connected if there is a path from u to v and a path from v to u.
vertexes that share this property can be parition into a disjoint set, where each disjoint set is a “strongly connected componet” From any node in the set you can get to any other node in the set.
Merging “Strongly Connected Components” into a meta-node will leave a dag. Every directed graph is a dag of it’s strongly connected components.
Strongly Connected Component Algorithm
Time:
Algo:
Time: Linear O(|E| + |V|)
Algo:
- Reverse the graph and run DFS with pre/post numbers.
- Select numbers from Highest post number to least, this gives us Source nodes for the Reverse Graph, which are actually sink nodes for the regular graph which is what we want.
- Do a BFS from the first node in the list and remove everything it connects to. That is the first strongly connected component. Then repeat with the next highest number remaining in the list.
Breadth First Search
Time:
Def:
Time: O(|V| + |E|) Linear.
Initially the queue Q consists only of s, the one node at distance 0. And for each subsequent distance d = 1, 2, 3, . . . , there is a point in time at which Q contains all the nodes at distance d and nothing else. As these nodes are processed (ejected off the front of the queue), their as-yet-unseen neighbors are injected into the end of the queue.
Dijkstra’s Algorithm
Time
Defn
Based on Priority Queue (min heap/Binary)
O( (|V| + |E|) log|V|)
Dijkstra is a version of BFS, but uses a priority queue to prioritize node traversal basedon edge length.
Note: As each node is traversed it keeps a back pointer to it’s predecessor, this way the path back to the shortest can simply traverse back the pointers.
NOTE: NO NEGATIVE VALUES ALLOWED!
Algorithms capable of finding shortest paths with negative weights.
Reminder: Negative weight cycles can be detected in some cases using these algorithms.
Bellman Ford = O(|V| * |E|)
Minimum Spanning Tree
Def
Time
Take a graph and find the minimum weighted, acyclic tree, that keeps all nodes connected without introducing cycles.
2 Algorithms: Kruskal and Primm.
Kruskal’s algorithm
time
def
O(|E| Log |V|).
Start with an empty graph and repeatedly add the next lightest edge that doesn’t produce a cycle.
(Based on Cut Property)
union by rank - starts with disjointed sets and does find and combine in log(n) time.
Cut Property
In building a minimum spanning tree, if we connect two minimum spanning trees using the lightest edge between the two of them, the result is a new minimum spanning tree.
Prim’s Algorithm
Time
Def
O(m log n)
Each iteration the smallest edge on the frontier is added to the tree, provided it doesn’t create a cycle.
(Almost identical to dijkstra, except dijkstra uses the full path length to the node as it’s key in the priority queue. Prim, only uses the weight of the indiviual edge on the frontier when it is added to the priority queue.)
Max Flow - Min Cut
Time
Def
Time: O(C * |E| )


