General Form of Cauchy's Theorem Flashcards
(19 cards)
Define winding number.

Finish the following theorem.


Finish the following lemma about winding numbers.
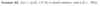
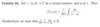
Prove the following lemma.
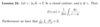

Finish the following proposition.
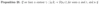
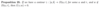
Prove the following proposition.
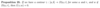
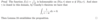
Define homologous to zero.

Define simply connected.

Define a cycle.
A cycle is a formal sum of closed contours Γ = Ɣ1 + Ɣ2 + ….. + Ɣn
Define the winding number of Γ around w.

Define the line intergral of f over Γ.
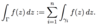
When is a cycle Γ homologous to zero in U?
If for every w ∉ U we have that I(Γ;w) = 0.
What is the General Form of Cauchy’s Integral Formula, and Cauchy’s Theorem?

How do you obtain the old CIF from the generalsied one?

Define simple.

What is Jordan’s curve theorem?

Given a simple closed contour Ɣ it is possible to put an orientation on Ɣ such that for all w ∈ ℂ \ Ɣ we have that?

Define when f if holomorphic on DƔint ∪ Ɣ.

What is Cauchy’s Integral Formula and Cauchy’s theorem for simple closed curves?