Application of Cauchy's Integral Formula in general form. Flashcards
(18 cards)
What is the Laurent Series Expansion of f proposition?
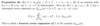
What is the uniqueness and existence of the Laurent series theorem?

Prove the following theorem.


Define the principal part of f.

What are the three types of singularities?
- Removable singularity at a
- f has a pole or order k at a
- f has an essential singularity at a
What is meant by f has a removable singularity at a?
f has a removable singularity at a if cn = 0 for all n ≤ −1, that is the principal part of f is zero, then we say that f has a removable singularity at z = a.
What is meant by f has a pole of order k at a?
If there exists a k > 0 such that c-k ≠ 0 and cn = 0 for all n < - k they we say that f has a pole of order k at z = a.
What is meant by f has an essential singularity at z=a?
When there are infinitely many n < 0 such that cn ≠ 0 then we say that f has an essential singularity at z = a.
How do the type of singularities relate to the principle part of f?
- Removable singularity at a - no principal part
- f has a pole or order k at a - the principal part is not zero
- f has an essential singularity at a - principle part is an infinite series
Finisht the following proposition.
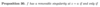
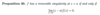
What is the proposition about equivalent conditions for f to have a pole at a?

What is a way to think of zeros and poles?
Zeros are where the numerator is zero, poles are where the denominator is zero.
Define a residue.
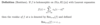
Finish the following proposition.
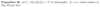
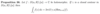
What is Cauchy’s Residue Theorem for simple closed curves?
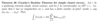
Define meromorphic.

What is Cauchy’s Residue theorem?

What are the four rules for calculating residues?



