Functions Flashcards
Compound Interest Formula
f(t) = P (1 + r/n)nt
logb1 =
0
logbb =
1
logbbp =
p
logbMN =
logbM + logbN
logb(M/N) =
logbM - logbN
logbMp =
p logbM
Exponential Growth or Decay Formula
f(t) = a(1 + r)t
- a is the current or initial count
- r is the growth or decay rate
- t is time.
Identify the Function
Absolute Value Function
Identify the Function
Cubic Function
Identify the Function
Identity Function
Identify the Function
Linear Function
Identify the Function
Square Root Function
Identify the Function
Quadratic Function
Identify the Function
Logarithmic Function
Identify the Function
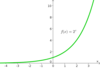
Exponential Function
Identify the Function
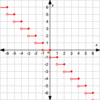
Step Function
Rule for translating a function horizontally
f(x ± k)
- k shifts right
- k shifts left
Rule for translating a function vertically
f(x) ± k
- k shifts up
- k shifts down
Rule for stretching or compressing a function vertically
(k × f(x))
- k > 1, stretch
- 0 k < 1, compress
- - k, reflected about x-axis
Rule for stretching or compressing a function horizontally
( f(k × x))
- k > 1, compress
- 0 k < 1, stretch
- k, reflected about y-axis
Theorem that states every non-constant, single variable polynomial has exactly as many roots as the polynomial’s highest exponent.
Fundamental Theorem of Algebra
Theorem which states that if a polynomial finction f(x) is divided by a binomial x-a, where a is a real number, the remainder of the division will be the value of f(a). If f(a) = 0, then a is a root of the polynomial.
Remainder Theorem
Theorem which states that if f(a) = 0 then (x - a) is a factor of the function.
Factor Theorem
Theorem which states that any rational root of a polynomial function
f(x) = anxn + an-1xn-1 + … + a1x + a0
with integer coefficients will, when reduced to its lowest terms, be a positive or negative fraction such that the numerator is a factor of a0 and the denominator is a factor of an.
Rational Root Theorem
Define these properties of functions:
- End Behavior
- y-intercept
- Roots
- Extrema
- The behavior of the function at extreme values (f(x) as x → ± ∞)
- The value of the function at f(0)
- The value of x where the function equals zero (f(x) = 0
- Minimum or maximum values of the function or where the function changes direction (f(x) ≥ k) or (f(x) ≤ k)
Define:
Function
A relation in which each value of x has exactly one value for y on the coordinate plane.
Define:
One-to-one Function
A relation in which each value of x has exactly one value for y on the coordinate plane and each value of y has exactly one value for x.
The vertical line test will determine if a graph is a function.
The horizontal line test will determine if it is one-to-one.
Define:
Many-to-one Function
A function whereby the relation is a function, but the inverse of the function is not a function. Each element in the domain is mapped to one and only one element in the range. However, one or more elements in the range may be mapped to the same element in the domain.
Define:
Monotone Function
A function whose graph either constantly increases or constanyly decreases.
Define:
Even Function
A function whose graph is symmetric with respect to the y-axis and satisfies the equation f(x) = -f(-x).
Define:
Odd Function
A function whose graph is symmetric with respect to the origin and satisfies the equation f(x) = -f(-x).
Define:
Constant Function
A function given by the equation f(x) = b where b is a real number. There is no independent variable present in the equation, so the function has a constant value for all x.
Define:
Identity Function
A function defined by the equation f(x) = x, where every value of the function is equal to its corresponding value of x. The only zero is the point (0,0). The graph is a line with slope of 1.
Define:
Linear Function
A function whose value changes in direct proportion to x. The rate of change, represented by the slope of its graph, is constant throughout.
Define:
Algebraic Function
