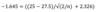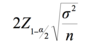Final - Multiple Choice Questions Flashcards



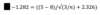
A researcher is told that if the E. coli concentration in the water exceeds the threshold, a notice has to be sent out to stop water consumption so that no one gets sick. What would be the result of a Type I error?
- Sending a notice when there shouldn’t be
- Incorrect rejection of a true null hypothesis (the E. coli concentration does not exceed the threshold in reality, but is thought to)
A researcher is told that if the E. coli concentration in the water exceeds the threshold, a notice has to be sent out to stop water consumption so that no one gets sick. What would be the result of a Type II error?
- Not sending a notice when there should be
- Type II error is incorrectly retaining a false null hypothesis (supposing that the E. coli concentration does not exceed the threshold, but in reality it does)
A researcher is told that if the E. coli concentration in the water exceeds the threshold, a notice has to be sent out to stop water consumption so that no one gets sick. How does increasing B affect the outcome of the population?
Increases the risk of people getting sick
How does an increase in B affect the power of the test? How does that affect the risk of a Type II error?
- Decreases the power of the test
- Increases the risk of a Type II error
A researcher is told that if the E. coli concentration in the water exceeds the threshold, a notice has to be sent out to stop water consumption so that no one gets sick. Does raising or lowering the power of the test reduce the risk of people getting sick?
Raising the power of the test
True or False: In the ANOVA for an RCBD with 4 replicates per treatment per block, the main effects of the block factor, Bj (j=1,…,n) are i.i.d. N(uB2, 0).
False
True or False: In the ANOVA for an RCBD with 4 replicates per treatment per block, if the treatment-by-block interaction is significant, the sum of squares for a “new error term” must be calculated.
False, the “new error term” is only calculated if the interaction is NOT SIGNIFICANT.
True or False: In the ANOVA for an RCBD with 4 replicates per treatment per block, the number of degrees of freedom of the “new error term” is obtained by adding the numbers of degrees of freedom for the interaction and the initial error term.
True
True or False: In the ANOVA for an RCBD with 4 replicates per treatment per block, when the ranking of mean values per treatment is the same over all blocks, there is potential for a treatment-by-block interaction.
False
True or False: An estimator θˆ of the population parameter θ is said to be unbiased and precise if E(θˆ − θ) = 0 and Var(θˆ ) is small.
True
True or False: By definition, the analysis of variance F-test is always one-tailed.
True
True or False: When testing H0: p = 0.30 against H1: p < 0.30, H0 is rejected when the observed value of the test statistic zobs is less than –z1-α.
True
True or False: In a case with two random samples and one qualitative dichotomous variable, the statistical analysis can be done using a chi-square test of independence or a test of two population proportions.
False
True or False: When testing H0: μ = μ0 against H1: μ > μ0, with σ2 known, the null hypothesis cannot be rejected when tobs is smaller than t1-α.
True, when σ2 known, use the Z-table
True or False: If a 95% confidence interval for μ is calculated to be [7, 9], with X ∼ N (μ, σ2), then the probability that μ is smaller than 7 is 0.05.
False, it is 0.025
True or False: If, on average during a certain period, it rains in Ste-Anne 3 times a week, then the number of times it rains in 3 weeks (X) follows a Poisson distribution with E(X) = Var(X) = 9.
True
Var(X) = E(X) = m = (3)(3) = 9
True or False: By only increasing the sample size (n), you also increase the confidence level (γ) of a confidence interval if the values of the lower and upper bounds remain unchanged.
False
True or False: If some H0 is rejected against some H1 at α = 0.05, then the same H0 is automatically rejected against the same H1 at α = 0.01.
False
True or False: A statistically significant positive linear correlation between X and Y necessarily implies that if you run an experiment in which X is decreasing, then Y should respond by increasing automatically.
False
True or False: Using blocks in an RCBD with 1 replicate per treatment per block will reduce the Error SS, relative to a CRD, in the ANOVA decomposition.
True
True or False: In a chi-square test of independence for a 4 x 3 contingency table, H0 is rejected at α = 0.05 when the observed value of the test statistic is greater than χ20.95(5).
False, it is rejected when the observed value is greater than χ20.95(6).
True or False: When performing a t-test to assess the difference between means using two independent random samples ( H0 : μA = μB ), an effective number of degrees of freedom needs to be calculated if the variances are assumed to be equal.
False