FI: Measurements of Interest Rate Risk Flashcards
Duration/convexity approach vs Full valuation =
Full valuation is preferable - this means considering changes in shape of the yield curve, models for embedded options (inclusive of interest rate vol)
(for a simple example full valuation will just be plugging the numbers into the calculator, changing ‘i’ to get the new PV)
The duration/convexity approach assumes parallel shifts in the YC - it provides a simpler way to estimate interest rate risk.
Price-yield relationship: regular bond =
POSITIVE CONVEXITY
price and yield are inversely related
this line is positively convex - it increases in price more when yields fall than it decreases in price when yields rise.
As a result, duration is lower at higher market yields (points further right on the curve) because the price of a bond decreases at a decreasing rate.
Price-yield relationship: callable bond =
NEGATIVE CONVEXITY
the call option limits the price upside.
when the price begins to rise at a decreasing rate (as yields get lower) the price-yield curve bends and exhibits NEGATIVE CONVEXITY (the curve will still have positive convexity at higher yields)
this effect is similar for PREPAYABLES - note that at lower yields (negative convexity region) the REINVESTMENT RISK rises along with the PREPAYMENT RISK - it is more likely that there will be principal repayments to reinvest.
Price-yield relationship: Putable bond =
value of a put increases at higher yields, decreases at lower yields - the holder of the bond wants to have a put option when market yields have risen and his bond has fallen in value.
this makes the price-yields relationship even FLATTER AT HIGHER YIELDS - there is less sensitivity to changes in yields
AT LOWER YIELDS (left of y’ in the graph) a putable bond will act like an option free bond in response to changes in yield
EFFECTIVE DURATION (formula) =
uses the average of the price changes for equal increases and decreases in yield.
not that for a bond with no options MODIFIED DURATION and EFFECTIVE DURATION will be approximately the same
PERCENTAGE CHANGE IN BOND PRICE =
-effective duration x yield change in %
Comparing duration measures =
why effective duration is most appropriate for bonds with embedded options…
effective duration is the preferred duration measure as it gives a good approximation for both regular and embedded option bonds.
Macauley duration =
estimate of a bonds’ interest rate sensitivity based on the time, in years, until promised cash flows will arrive.
earliest form of duration.
example - duration for a 5yr zero is 5years. duration for a 5yr annual coupon bond is less than 5years. consistent with the principle that higher coupon means lower duration.
–> wieghted average of the time until each cash flow wil be received (with each cash flow weighted by its proportion of the total bond value)
IT IS NOT APPROPRIATE FOR BONDS WITH EMBEDDED OPTIONS
Modified duration =
derived from macauley duration but takes into account the current YTM
just as macauley, NOT APPROPRIATE FOR BONDS W/ EMBEDDED OPTIONS
modified and effective duration will be very similar for bonds with no embedded options.
modified duration considers the curvature of a regular bond’s yield-price relationship - the denominator increases as yield increases, decreasing duration - so that at higher yields, duration is lower.
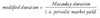
Interpreting duration =
- slope of the price-yield curve ie. first derivative
- macauley duration - weighted average time to receipt of cash flows
- sensitivity of a bond’s price to a 1% change in yield (PREFERRED INTERPRETATION)
Portfolio duration and limitations =
simply a weighted average of the durations of each bond.
LIMITATIONS: not every bond’s yield will change at the same time or by the same amount ie. the YC may steepen, meaning longer bonds’ yields change while short bonds’ yields remain the same.
this is the same limitation that we encounter for an individual bond, that DURATION IS A GOOD MEASURE FOR PARALLEL SHIFTS IN THE YIELD CURVE.
Convexity =
measure of the curvature of the price-yield relationship.
more curved = greater convexity
if the price-yield relationship is a linear (convexity = 0) then duration is a good approximation on its own - as the graph shows, it will underestimate the price (underestimate price change on the upside and overestimate it on the downside) when convexity is positive.
THE GREATER THE CONVEXITY, THE GREATER THE ERROR IN PRICE ESTIMATES BASED SOLELY ON DURATION.
duration and convexity : EQUATION =
change in yield MUST BE IN DECIMAL
note: when convexity is positive, the change in price attributed to convexity is always positive (regardless if yields increase or decrease, given the delta y squared) - reflecting that duration underestimates prices resulting from both increases and decreases in yields - and convexity adjusts for this.
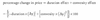
Effective and modified convexity =
same as effective and modified duration - modified duration does not take into account the possibility that cash flows may vary due to embedded options
PVBP, DVO1 =
price value of a basis point (chang in yield)
= duration x 0.0001 x bond value
