Dr Musa Flashcards
What are differential equations?
A differential equation is an algerbraic or transcendental equation which involves derivatives
What are transcendental equations?
Give some examples
These are equations containing transcendental functions i.e. they transcend algebra. They cannot be expressed in terms of finite sequence of the alegebraic operations of addition, multiplication and root extraction.
Expontential functions, (ex, xπ) logarithmic (log (x)) and trionometric functions (sin(x), cos(x)) are example of transcendental functions
What are difference equations
A difference equation is an algebraic or transcendental equation which involves a dependent variable, say y(k), defined on a discrete set of the independent variables, say x(k), where k is the integer-valued discrete time variable
Differential equations relate to ____-____ ____ in the same sense as difference equations relate to ____-____ ____
Differential equations relate to continuous-time systems in the same sense as difference equations relate to discrete-time systems
What is an ordinary differential equation?
An equation involving;
- One independent variable
- One or more dependant variable, and
- One or more derivatives of the dependent varable with respect to the indedpendent variable
What is a partial differential equation?
An equation involving;
- Two or more independant variables
- One or more dependent varibles, and
- One or more partial derivatives of the dependent variable (or variables) with respect to the independent variable
What is a term of a differential equation?
An explicit function of the independent variable, the dependent variable and the derivatives of the dependent variable
What is a term of a difference equation?
A product and/or quotient of an explicit function of the independent variable and the dependent variable
What is a linear term in a differential equation?
A term whose degree in the dependent variable or their derivatives is 1 (i.e. raised to the power - or degree - or 1)
What is a linear differential equation?
A differential equation consisting of only linear terms
The class of linear differential equations where ai and bi are constants is called…
and these equations represent…?
…Linear differential equations with constant co-efficients and these equations represent linear time-invarient systems
y=y(t) is often called the ____ or the ____ of the system, and is the ____ solutions fo the differential equation to be determined.
Whereas u=u(t) is often called the ____, and is a ____ (or ____) function
y=y(t) is often called the output or the response of the system, and is the unknown solution fo the differential equation to be determined.
Whereas u=u(t) is often called the input, and is a known (or given) function
For physical systems, m ? n and n is the ____ of the diff eqn
m ≤ n and n is the order of the diff eqn
The class of linear difference equation where ai and bi are constants is called…?
…linear difference equations with constant coefficients
Diff/diffence equations that are not linear are called…?
…non linear differential/difference eqns
What is the order of a diff eqn?
The order of a diff equation is the order of the highest derivative appearing in it
What is the order of a difference eqn?
The difference between the largest and the smallest arguements of the interger-valued discrete variable appearing in it
What is the degree of a diff eqn?
The degree of a diff eqn that can be written as a polynomial, in the derivatives is the degree of the highest ordered derivatives that appear in it
What is a differential operator?
When you replace d/dt with a symbol or a letter, say D
An equation or polynomial containing a differential operator is called…?
…the auxiliary or characteristic eqn
D3+D2+2=0
Linear differential equation of the form:
is called a…?
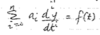
homogeneous nth-order linear differential equation if f(t) = 0; otherwise it is non homogeneous
dy/dt + ry = ? in terms of D
and so D = ?
And then this solution can be wirtten as;
y = ?
(D+r)y = 0
D = -r
y = CeDt
If D
Therefore, the system is ____
If D decays as t…tends to infinity.
Therefore, the system is stable
If D
Therefore, the system is ____
If Dincreases unboundelly as t tends to infinity.
Therefore, the system is unstable
If the (b2-4ac) > 0, the roots of the characteristic equation D1 and D2 are ____ and ____ (i.e. ____)
With the general solution being;
y = ? + ?
If the (b2-4ac) > 0, the roots of the characteristic equation D1 and D2 are real and distinct (i.e. unequal)
With the general solution being;
y = c1eD1t + c2eD2t
If (b2-4ac) = 0 then the roots of the characteristic are ____ and ____
The general solution is
y = ? + ?
If (b2-4ac) = 0 then the roots of the characteristic are real and equal
The general solution is
y = c1eD1t + c2teD2t
If (b2-4ac)
The general solution is
y = ? + ?
If (b2-4ac) complex numbers
The general solution is
y = K1eD1t + K2e<span>D2t</span>
Using Eulier’s identity the last expression can be simplified to
y = eøt(c1 cosßt + c2 sinßt)
Where c1 = K1 + K2
c2 = j(K1 - K2)
2nd-order systems have _ inital conditions, an nth-order system will have _ inital conditions
2nd-order systems have 2 inital conditions, an nth-order system will have n inital conditions
y’’’ - y’ = 0
It’s characteristic equation is…?
D3 - D = 0
Define steady state response
The point of the total response that does not approach zero as time approaches infinity
Define transient response
The point of the total response that approaches zero as time approaches infinity
y(t) = ya(t) + yb(t)
What is the forced response and what is the free response?
y(t) = ya(t) + yb(t)
ya is the free response
yb is the forced response
yb(t) = ∫ w(t-J)
What is w(t-J) called?
The weighting function or the kernal of the differential equation
This is provided in the data booklet, but what would the Laplace transform of a single-sided or unilateral look like?
Where would it be useful?
The change in ∞ to 0t
This would be particularly useful for finding the Laplace transform of functions that are discontinuous at t=0
In Laplace transform, L is called the…?
Laplace transform operator
What is Euler’s Identity?
eajt = cos(at) + j sin(at)
Time scaling: If the Laplace transform of a function x(t) is x(s), then the Laplace transform of the function x(at) is given by…
L{x(at)] = 1/a . X(s/a)
If you have an equation like this, what should you do?
- Factorise
- Partial fraction
Division by t: If the Laplace transform of a function x(t) is X(s), then the Laplace transform of x(t)/t is given by…
L{x(t)/t}= ∞∫s X(u)du
Frequency scaling property: If x(s) is the inverse Laplace transform of x(t), then the inverse Laplace transform of x(ks) is…?
1/k.x(t/k)
What is the complex convolution intergral of x1(t) and x2(t) ?
The first term of on the right of the equation is the ____ ____ and the second term is the ____ ____ of the system
The first term of on the right of the equation is the forced response and the second term is the free response of the system
The transfer function of a LTI system is the point of the first term in the right side of the equation multiplying U(s)
Define the transfer function of a LTI system
The ratio of the Laplace transform of the output variable Y(s) to the Laplace transform of the input variable U(s), with all initial conditions assumed to be zero
The output of any continuous-time LTI system is the…?
…convolution of the input with the impulse response of the system
What are the roots of the characteristic equation called?
Poles
What are the roots of numerator polynomial of the transfer function called?
Zeros
When is the system stable?
If all of the roots of the characteristic equation (that is the system poles) have negative real point/parts
The transfer function, G(s) = ?
G(s) = Y(s) / U(s)
What is the characteristic equation in this equation?
Characteristic equation: s2+4s+3
The characteristic equation is the…?
…denominator
If the input is a unit step function, u(t) = 1, so
u(s)?
u(s) = L{u(t)} = 1/s
If the input is a unit impluse function, ∂(t) = u(t) = ?
∂(t) = u(t) = 1
What are Fourier seires?
Fourier series are infinite series designed to represent general periodic functions in terms of cosines and sines
In the Fourier series, wo = ?
And To = ?
wo = 2π/To
To = 2L
In Fourier series, f(t) = ?
The Fourier coefficients given by the so-called Euler formulas
an = ?
bn = ?
In the Fourier series,
a0 = ?
The graph of an even function is symmetric with respect to the…?
…y-axis
The graph of an odd function is symmetric about the…?
…origin
The intergral of an even function over a symmetric interval (-a,a) is ____ the intergral of that function over (0,a), that is, if f(t) is an ____ function then…
The intergration of an even function over a symmetric interval (-a,a) is twice the intergral of that function over (0,a), that is, if f(t) is an even function then…
The intergral of an ____ function over a symmetric interval (-a,a) is zero. If g(t) is an ____ function then…
The intergral of an odd function over a symmetric interval (-a,a) is zero. If g(t) is an odd function then…
The Fourier series of an even function is a “Fourier ____ series” because the Gourier coefficients bn are all identically equal to ____
The Fourier series of an even function is a “Fourier cosine series” because the Gourier coefficients bn are all identically equal to zero
The Fourier series of an odd function is a “Fourier ____ series” because the Fourier coefficients an, including a0, are all identically equal to ____
The Fourier series of an odd function is a “Fourier sine series” because the Fourier coefficients an, including a0, are all identically equal to zero
What is the equation for the avergae power P of a periodic signal x(t) over any period?
where denotes the fundamental period of x(t)
What is Parseval’s Identity for Fourier series?
State Parselva’s Identity with proof
If an and bn are the Fourier coefficient components dying down to f(x) and if f(x) satifies the Dirichelet conditions
