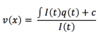Dr Griffiths Flashcards
Define a function
A function is a rule which operates on an input and produces a single output
What do you do to the number of a;
“One-to-one” rule?
“Many to one”?
“One to many”?
“One-to-one” - Multiply by 1
“Many to one” - Square the numbers
“One to many” - Take the square root
“One to many” is not an exmaple of a ____
Why?
Function
Because one input produces more than one output
A function has a ____ and ____
domain** and **range
Define domain
A set of values we allow the independant variable to take
Define the range
The set of y-values in the domain
Functions can also be described…?
Define it
Parametrically : One of a set of independent variables that express the coordinates of a point
Real life example of continuity?
Can you keep your pen on the paper when drawing the curve?
A function is ____ if it is not continuous
discontinuous
In the unit step function,
v(t) = ? if t ≥0
v(t) = 0 if t ? 0
v(t) = 1 if t ≥0
v(t) = 0 if t < 0
A function that has a definite pattern repeated at regular intervals is said to be…?
e.g.?
Periodic
e.g. y=sinx
A function f(x) is ____ if we can find a number ‘T’ such that
f(x+t) = ? for all x
A function f(x) is periodic if we can find a number ‘T’ such that
f(x+t) = f(x) for all x
A function that is symetric about the _-axis is said to be…?
y-axis is said to be even
A even function is such that
f(-x) = ? for all of x
f(-x) = f(x) for all of x
A odd function is such that
f(-x) = ? for all of x
f(-x) = -f(x) for all of x
An exponential function has the form y = ?
y = ax
y = 2x - derivative lies ____ the curve
y = 3x - derivative lies ____ the curve
y = 2x - derivative lies below the curve
y = 3x - derivative lies above the curve
3! = ?
3! = 3x2x1 = 6
ex - exponential ____ as x → ?
e-x - expontential ____ as x → ?
ex - exponential growth as x → ∞
e-x - expontential decay as x → ∞
e always…?
dominates
If y=ex then x = ?
x = ln(y)
If it’s ex + ex then it’s ?
But if its ex - e-x then it’s ?
Even
Odd
tanh(x) = ?
coth(x) = ?
sech(x) = ?
cosech(x) = ?
tanh(x) = sinh(x)/cosh(x)
coth(x) = 1/tanh(x)
sech(x) = 1/cosh(x)
cosech(x) = 1/sinh(x)
The three different types of stationary points are…?
- Maximum point
- Minimum point
- Points of inflection
Maximum and minimum points can either be ____ or ____
local** or **global
Minimum point if d2f/dx2 is…?
Maximum point if d2f/dx2 is…?
Minimum point if d2f/dx2 is > 0
Maximum point if d2f/dx2 is <0
If d2f/dx2 = 0 …? so we need to?
we need more information.
So we need to evaluate the sign of the function f(x) near to the point x=xs
Any change in sign reveals a…?
point of inflection
The Maclaurin series always expands about the point…?
x=0
Maclaurin series = Taylor series about…?
x=0
e = ?
e = 1 + 1/1! + 1/2! + 1/3! + … 1/n!
The limit of f(x) is _ as x approaches a, and is written as…?
The limit of f(x) is L as x approaches. This is written as
limx→a f(x) = L
L’Hôpital’s Rule, if
f(x)/g(x) = 0/0
you do what?
Just differentiate both lines
f’(x)/g’(x)
A sequence is simply…?
…a sucession of numbers
A series is…?
…simply the sum of the terms of the sequence
If the sequence of partial sums converges then we say that…??
…the series converges
What would be the first thing to spot in something like this?
I = ∫ sin(x) cos(x) dx
That if you dy/dx sin(x) then you get cos(x) so
d(sin(x))/dx = cos (x)
so sub in the bold part into the previous equation for cos(x)
Tricky intergrates can often be simplified by…?
…using a suitable substitution
The mean value of a function f(x) between points A and B is…?
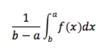
The root means square value of a function f(x) between points A and B is…?

The RMS (____ ____ ____) value is used when…?
The RMS (Root mean square) value is used when… determining the strength of voltage supplies
What is the area of a circle?
πr2
A solid rotating about the x-axis,
r = ?
Equation is v =
r=y
v =
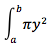
Rotating about the y-axis,
r = ?
Equation v = ?
r = x
v =
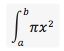
How do you measure the length of a curve? (Eqn)
Simply apply pythagoras’ theorem to determine the length of a hypotenuse (kinda)
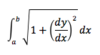
An explicit function has the form y = ?
Whereas an implicit function has the form…
Explicit y = f(x)
Implicit f(x,y) = 0
y = arcsin(x)
What does x = ?
x = sin(y)
We can use the idea of implicit differentiation to determine the…
…derivative of logarithmic type functions
Define Partial differentiation
Partitial differentiation is define as the rate of change of a function of multiple variables, with respect to one (or more) independant variables
∂ = ?
d = ?
∂ = Many
D = One
When taking the partial derivative with respect to one independant variable the others are viewed as…?
…constants
fxx means?
Differentiate with respect to x twice
Stationary points occur when…?
df/dx = 0
What would functions of two variables look like?
= fxxfyy - f(xy)2
If D < 0 = ?
If D > 0 and fxx > 0 = ?
If D > 0 and fxx < 0 = ?
If D = 0
If D < 0 = Saddle point
If D > 0 and fxx > 0 = Minimum point
If D > 0 and fxx < 0 = Maximum point
If D = 0 - We need some more info
D = ?
f(xy) = ?
D = fxxfyy - f(xy)2
f(xy) = 0 (for whatever reason)
j = ?
√-1
j is the…
…‘Imaginary number’
In general, we write complex numbers in the form;
z = 1 +- j
The modulus of a complex number is…?
|z| = √(a2+b2)
Give an example of a complex conjugate pair
z = a + bj
z* = a - bj
What do you plot complex numbers on?
An Argand diagram
On an Argand diagram, what is the x and y-axis?
x-axis = real part of z
y-axis = imaginary part of z
For complex numbers,
x = ?
y = ?
x = rcos(ø)
y = rsin(ø)
In an argand diagram when plotting complex numbers, what parts of the diagram do you add or minus π?
3rd = -π
2nd = +π
ø > π other way round
What is Elver’s identity?
ejπ + 1 = 0
rejø = ?
rejø = r(cos(ø) + jsin(ø))
What is De Moivre’s theorem?
cos(nø) + jsin(nø) = [cos(ø) + jsin(ø)]n
In De Moivre’s theorem,
cos(nø) + jsin(nø) = ?
cos(nø) + jsin(nø) = [cos(ø) + jsin(ø)]n
De Moivre’s theorem is particulary useful for…?
…finding roots
Non linear homogeneous equations = ?
Linear non-homegneous = ?
NLH = 0
LNH = x2
The function I(x) is known as…?
The intergrating factor
For first ODE’s, what do we want it to look like?
dy/dx + yp(x) = q(x)
I(x) = ?
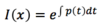
In first ODE’s, v(x) = ?