Distribution Theory Flashcards
Define a probability density function.
Define a cumulative distribution function.
Define expectation and variance.
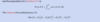
What is the pdf for the uniform distribution?
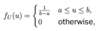
What is the cdf for the uniform distribution?
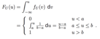
What is the standard uniform distribution?
a = 0, b = 1 so U ∼ u(0,1)
What is the pdf and cdf of the standard uniform distribution?
- fu(u) = 1
- Fu(u) = u
How do you derive the cdf of the exponential using the Poisson distribution?
What is the pdf of the exponential distribution?
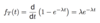
How do you find the pdf of the exponential distribution, once you have derived the cdf?
Differentiate it
What is a similarity between the exponential and gamma distribution?
- Exponential is the time until the first event occurs
- Gamma is the time until the nth event occurs
How do we derive the cdf of the Gamma distribution?
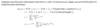
Given the cdf of the Gammas distribution, differentiate it to find the pdf.
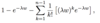
Define the Gamma distribution.
What does Γ(1/2)
sqrt(π)
What does Γ(n) equal when n i an integer?
(n-1)!
What are three properties of the Gamma distribution?
Prove the 𝔼(W) = α/β for the Gamma distribution.
What does the pdf and cdf look like for U ∼ u[a,b]?
What does the pdf and cdf look like for T ∼ Exp(λ)?
What does the pdf and cdf look like for W ∼ Ga(α,β)?
If we have a continuous random quantoty X with pdf fX(x), and y = g(x) what are the two methods to find the distribution and denisty of Y?
- The cumulative distribution function method
- The change of variables theorem.
What are the two steps in the cumulative distribution method?
What pdf fX(x) and function g(X) do you combine to get the a chi squared distribution?
Z ∼ N(0,1) then Y = Z2
How do you derive the cdf of the Chi-squared distribution using the cumulative distribution function method?
What are three properties of the chi-squared distribution?
What is the univariate transformation theorem?
Prove the following theorem.
What is the probability integral transform theorem?
Prove the following theorem.
What is an important use of the probability integral transform theorem?
Inverse sampling - we can generate random numbers from (almost) any distribution by applying an appropiate transformation to a simple standard uniform random numbers
What is the algortihm for inverse sampling?
Define a joint pdf.
Define a joint cdf.
Define a marginal pdf.
Define a conditional pdf.
Define independence between two random quantities.
If you have a dsitribution f(x,y) how do you find the marginal distribution fo fX(x)
Integrate with respect to y
What is the multivariate transformation theorem?
What is the 100(1-α)% CI for μ using s from a sample?
What do we use when we don’t know a value for σ?
s
What is the formula for s?
When is it wrong to use s?
When s ≠ σ, it will lead to a very wrong confidence interval.
What is the Lemma about the following?
What is a corollary that links Ẍ and S2?
What is the theorem about the Sampling distribution of S2?
Prove the following theorem.
What is the 100(1 - σ)% confidence interval for σ2?
Define a t distribution.
What are four properites of the t distribution?
What is the theorem about ?
Prove the following theorem.
What is the confidence interval for μ when σ2 is unknown?
As n ➝ ∞ what does the t distribution tend to?
The normal
