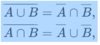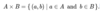Discrete Math Flashcards
(103 cards)
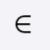
2 ∈ {1,2,3} asserts that 2 is an element of the set {1,2,3}.
In mathematics, an element, or member, of a set is any one of the distinct objects that make up that set.
Sets
Writing A = { 1 , 2 , 3 , 4 } {\displaystyle A={1,2,3,4}} means that the elements of the set A are the numbers 1, 2, 3 and 4. Sets of elements of A, for example { 1 , 2 } {\displaystyle {1,2}} , are subsets of A.
Sets can themselves be elements. For example, consider the set B = { 1 , 2 , { 3 , 4 } } {\displaystyle B={1,2,{3,4}}} . The elements of B are not 1, 2, 3, and 4. Rather, there are only three elements of B, namely the numbers 1 and 2, and the set { 3 , 4 } {\displaystyle {3,4}} .
The elements of a set can be anything. For example, C = { r e d , g r e e n , b l u e } {\displaystyle C={\mathrm {\color {red}red} ,\mathrm {\color {green}green} ,\mathrm {\color {blue}blue} }} , is the set whose elements are the colors red, green and blue.
Notation and terminology
First usage of the symbol ∈ in the work Arithmetices principia, nova methodo exposita by Giuseppe Peano.
The relation “is an element of”, also called set membership, is denoted by the symbol “ ∈ {\displaystyle \in } “. Writing
x ∈ A {\displaystyle x\in A}
means that “x is an element of A”. Equivalent expressions are “x is a member of A”, “x belongs to A”, “x is in A” and “x lies in A”. The expressions “A includes x” and “A contains x” are also used to mean set membership, however some authors use them to mean instead “x is a subset of A”.[1] Logician George Boolos strongly urged that “contains” be used for membership only and “includes” for the subset relation only.[2]
For the relation ∈ , the converse relation ∈T may be written
A ∋ x , {\displaystyle A\ni x,} meaning “A contains x”.
The negation of set membership is denoted by the symbol “∉”. Writing
x ∉ A {\displaystyle x\notin A} means that “x is not an element of A”.
The symbol ∈ was first used by Giuseppe Peano 1889 in his work Arithmetices principia, nova methodo exposita. Here he wrote on page X:
Signum ∈ significat est. Ita a ∈ b legitur a est quoddam b; …
which means
The symbol ∈ means is. So a ∈ b is read as a is a b; …
The symbol itself is a stylized lowercase Greek letter epsilon (“ϵ”), the first letter of the word ἐστί, which means “is”.
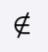
4 ∉ {1,2,3} because 4 is not an element of the set {1,2,3}.
The negation of set membership is denoted by the symbol “∉”. Writing
x ∉ A means that “x is not an element of A”.
{ 2 , 4 , 6 , 8 , 10 }
Finite or Infinite?
In mathematics, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
{ 2 , 4 , 6 , 8 , 10 }
is a finite set with five elements. The number of elements of a finite set is a natural number (a non-negative integer) and is called the cardinality of the set. A set that is not finite is called infinite. For example, the set of all positive integers is infinite:
{ 1 , 2 , 3 , … }
Finite sets are particularly important in combinatorics, the mathematical study of counting. Many arguments involving finite sets rely on the pigeonhole principle, which states that there cannot exist an injective function from a larger finite set to a smaller finite set.
{ 1 , 2 , 3 , … }
Finite or Infinite
In mathematics, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
{ 2 , 4 , 6 , 8 , 10 }
is a finite set with five elements. The number of elements of a finite set is a natural number (a non-negative integer) and is called the cardinality of the set. A set that is not finite is called infinite. For example, the set of all positive integers is infinite:
{ 1 , 2 , 3 , … }
Finite sets are particularly important in combinatorics, the mathematical study of counting. Many arguments involving finite sets rely on the pigeonhole principle, which states that there cannot exist an injective function from a larger finite set to a smaller finite set.
Ø
{ }
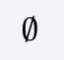
The empty set is the set which contains no elements.
In mathematics, the empty set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero.
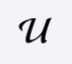
The universe set is the set of all elements.
In set theory, a universal set is a set which contains all objects, including itself.[1] In set theory as usually formulated, the conception of a universal set leads to Russell’s Paradox and is consequently not allowed. However, some non-standard variants of set theory include a universal set.

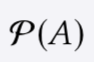
The power set of any set A is the set of all subsets of A.

The set of real numbers.
A real number is any positive or negative number. This includes all integers and all rational and irrational numbers. Rational numbers may be expressed as a fraction (such as 7/8) and irrational numbers may be expressed by an infinite decimal representation (3.1415926535…). Real numbers that include decimal points are also called floating point numbers, since the decimal “floats” between the digits.
Real numbers are relevant to computing because computer calculations involve both integer and floating point calculations. Since integer calculations are generally more simple than floating point calculations, a computer’s processor may use a different type of logic for performing integer operations than it does for floating point operations. The floating point operations may be performed by a separate part of the CPU called the floating point unit, or FPU.
While computers can process all types of real numbers, irrational numbers (those with infinite decimal points) are generally estimated. For example, a program may limit all real numbers to a fixed number of decimal places. This helps save extra processing time, which would be required to calculate numbers with greater, but unnecessary accuracy.
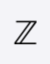
The set of integers. That is, Z {. . . , −2, −1, 0, 1, 2, 3, . . .}.
An integer is a whole number (not a fraction) that can be positive, negative, or zero. Therefore, the numbers 10, 0, -25, and 5,148 are all integers. Unlike floating point numbers, integers cannot have decimal places.
Integers are a commonly used data type in computer programming. For example, whenever a number is being incremented, such as within a “for loop” or “while loop,” an integer is used. Integers are also used to determine an item’s location within an array.
When two integers are added, subtracted, or multiplied, the result is also an integer. However, when one integer is divided into another, the result may be an integer or a fraction. For example, 6 divided by 3 equals 2, which is an integer, but 6 divided by 4 equals 1.5, which contains a fraction. Decimal numbers may either be rounded or truncated to produce an integer result.
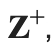
The set of integers. That is, Z+ = {1, 2, 3, . . .}.

The set of natural numbers. That is, N {0, 1, 2, 3 . . .}.
A natural number is an integer greater than 0. Natural numbers begin at 1 and increment to infinity: 1, 2, 3, 4, 5, etc.
Natural numbers are also called “counting numbers” because they are used for counting. For example, if you are timing something in seconds, you would use natural numbers (usually starting with 1). When written, natural numbers do not have a decimal point (since they are integers), but large natural numbers may include commas, e.g. 1,000 and 234,567,890. Natural numbers will never include a minus symbol (-) because they cannot be negative.
In computer science, natural numbers are commonly used when incrementing values. For example, in a for loop, the counter often increases by one with each iteration. Once the counter hits the limit (e.g., 10 in for (i=1; i<10; i++)), the loop is broken and the code after the loop is processed.
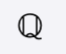
The set of rational numbers.
A rational number is any number that can be expressed as a ratio of two integers (hence the name “rational”). It can be written as a fraction in which the the top number (numerator) is divided by the bottom number (denominator).
All integers are rational numbers since they can be divided by 1, which produces a ratio of two integers. Many floating point numbers are also rational numbers since they can be expressed as fractions. For example, 1.5 is rational since it can be written as 3/2, 6/4, 9/6 or another fraction or two integers. Pi (π) is irrational since it cannot be written as a fraction.
A floating point number is rational if it meets one of the following criteria:
it has a limited number of digits after the decimal point (e.g., 5.4321)
it has an infinitely repeating number after the decimal point (e.g., 2.333333…)
it has an infinitely repeating pattern of numbers after the decimal point (e.g. 3.151515…)
If the numbers after the decimal point repeat infinitely with no pattern, the number is not rational or “irrational.” Below are examples of rational and irrational numbers.
1 - rational
- 5 - rational
- 0 - rational
√2 - irrational
3.14 - rational
π (3.14159265359…) - irrational
√4 - rational
√5 - irrational
16/9 - rational
1,000,000.0000001 - rational
In computer science, it is significant if a number is rational or irrational. A rational number can be stored as an exact numeric value, while an irrational number must be estimated.
NOTE: The number zero (0) is a rational number because it can be written as 0/1, which equals 0.
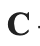
Based on the concept of real numbers, a complex number is a number of the form a + bi, where a and b are real numbers and i is an indeterminate satisfying i2 = −1. For example, 2 + 3i is a complex number.
This way, a complex number is defined as a polynomial with real coefficients in the single indeterminate i, for which the relation i2 + 1 = 0 is imposed. Based on this definition, complex numbers can be added and multiplied, using the addition and multiplication for polynomials. The relation i2 + 1 = 0 induces the equalities i4k = 1 , i4k+1 = i , i4k+2 = −1 , and i4k+3 = −i , which hold for all integers k; these allow the reduction of any polynomial that results from the addition and multiplication of complex numbers to a linear polynomial in i, again of the form a + bi with real coefficients a, b.
The real number a is called the real part of the complex number a + bi; the real number b is called its imaginary part. To emphasize, the imaginary part does not include a factor i; that is, the imaginary part is b, not bi.
Formally, the complex numbers are defined as the quotient ring of the polynomial ring in the indeterminate i, by the ideal generated by the polynomial i2 + 1 (see below).

{ x : x > 2 } is the set of all x such that x is greater than 2.
{ } = “set of”
x = “all x”
: = “such that” ( | = “such that as well”)
x > 2 = “x is greater than 2”

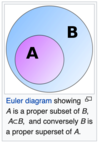
A ⊆ B asserts that A is a subset of B : every element of A is also an element of B.
In mathematics, a set A is a subset of a set B, or equivalently B is a superset of A, if A is contained in B. That is, all elements of A are also elements of B (note that A and B may be equal). The relationship of one set being a subset of another is called inclusion or sometimes containment. A is a subset of B may also be expressed as B includes A, or A is included in B.
The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra under the subset relation, in which the meet and join are given by intersection and union.


The cardinality (or size) of A is the number of elements in A.
In mathematics, the cardinality of a set is a measure of the “number of elements of the set”. For example, the set A = { 2 , 4 , 6 } contains 3 elements, and therefore A has a cardinality of 3. There are two approaches to cardinality – one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set is also called its size, when no confusion with other notions of size is possible.
The cardinality of a set A is usually denoted | A | , with a vertical bar on each side; this is the same notation as absolute value and the meaning depends on context.
A _____ produces a result from a pair of sets.
binary operation
A _____ produces an output from a single set.
unitary operation
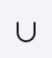
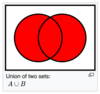
A∪B is the union of A and B: is the set containing all elements which are elements of A or B or both.
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection.[1] It is one of the fundamental operations through which sets can be combined and related to each other.
For explanation of the symbols used in this article, refer to the table of mathematical symbols.
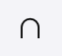
A ∩ B is the intersection of A and B: the set containing all elements which are elements of both A and B.
In mathematics, the intersection of two sets A and B or “A ∩ B”, is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements.[1]
For an explanation of the symbols used in this article, refer to the table of mathematical symbols.
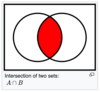
Let A = {1, 2, 3} and B = {4, 5, 6}
A ∩ B = Ø
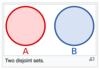
What kind of set pair is this?
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set. For example, {1, 2, 3} and {4, 5, 6} are disjoint sets, while {1, 2, 3} and {3, 4, 5} are not disjoint. A collection of more than two sets is called disjoint if any two distinct sets of the collection are disjoint.

The complement of A is the set of everything which is not an element of A.
In set theory, the complement of a set A refers to elements not in A.
When all sets under consideration are considered to be subsets of a given set U, the absolute complement of A is the set of elements in U but not in A.
The relative complement of A with respect to a set B, also termed the difference of sets A and B, written B \ A, is the set of elements in B but not in A.

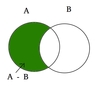
What is Set Difference?
Set Difference: The relative complement or set difference of sets A and B, denoted A – B, is the set of all elements in A that are not in B.
In set-builder notation, A – B = {x ∈ U : x ∈ A and x ∉ B}= A ∩ B’. You can also use the \ notation to define a set difference. A\B is the set of elements in A but not B.
The Venn diagram for the set difference of sets A and B is shown below where the shaded region represents A – B.
Example: Let A = {a, b, c, d} and B = {b, d, e}. Then A – B = {a, c} and B – A = {e}.
Source: http://web.mnstate.edu/peil/MDEV102/U1/S6/Complement3.htm

In mathematics, the symmetric difference, also known as the disjunctive union, of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by
A △ B ,
or
A ⊖ B ,
or
A ⊕ B .
For example, the symmetric difference of the sets { 1 , 2 , 3 } and { 3 , 4 } is { 1 , 2 , 4 }.
The power set of any set becomes an abelian group under the operation of symmetric difference, with the empty set as the neutral element of the group and every element in this group being its own inverse. The power set of any set becomes a Boolean ring with symmetric difference as the addition of the ring and intersection as the multiplication of the ring.