Derivatives Flashcards
(38 cards)
Delta
Sensitivity of option value to change in underlying price
can be seen as a slope of a line plotting the value of hte option against the underlying price
positive for long calls, negative for long puts
|Delta| for one option varies between 0 and 1
More OTM = closer to 0
More ITM = Closer to 1
ATM = around 0.5
underlying itself (or a future or forward on the underlying) has a delta of 1
Gamma
change in delta per +1 change in underlying stock price
positive for long calls AND long puts
greatest when ATM, and close to expiry
can be seen as the CURVATURE of a line plotting the value of hte option against the underlying price (vs. Delta, which is the slope of the same line)
Position Delta
net delta of a position (sum of deltas of all constituents, careful of plus or minus)
eg for a covered call:
own one stock and one stock worth of call
net delta is 1 - call delta
it’s “ 1-“ bc delta for the underlying itself (and futures and fwds) is +1 if you’re long, and -1 if you’re short … the delta of an underlying is obviously 1
Protective put:
1 - absolute value of the put delta (just because long puts have negative delta)
effective of an option reduces delta below 1
a delta-netural position is constructed to have total delta of zero, no net exposure to the underlying
Calls Basics
Long call = unlimited potential profit
Short call = unlimited potential loss

Puts Basics
max profit = breakeven price
breakeven when value = premium paid, when stock price = strike - premium

Protective Put
long the underlying, buy put
buying downside protection
unlimited upside
equivalent to synthetic long call

Covered Call + its applications
long underlying, sell a call
limited upside, most of the downside remains
receive option premium
Applications:
Yield enhancement –> calls OTM, hope that options expire OTM and keep premium
Reducing a position at a favorable price –> happy to sell the stock –> calls ITM, so likely stock will be sold
Target price realization –> calls marginally OTM –> you think stock worth a bit more than current price, happy to sell at slightly higher price

Collar
combo: own the underlying, buy put on lower strike, and sell call on higher strike
Buying downside protection PLUS selling off upside
net premium could be a pmt (debit) or receipt (credit)
limits exposure to the range btwn the two strikes
zero-cost collar = strikes selected so that premiums net to zero

Straddle
(and reverse straddle)
(Long) Straddle = buy call + put @ same strike –> profit from high volatility –> ideal when you expect large movement but dont know which direction
Reverse Straddle = sell call and put @ same strike –> profit from low volatility –> ideal when you think prices will be stable, minor moves up or down
2 breakeven points
Disadvantage: more up-front premium (have to pay for both call and put)
Advantage: max loss = premium, benefit

Bull Spreads
General spread info:
memory trick: BUY LOW SELL HIGH
both the same type of option (eg buy low call sell high call)
Spreads = buy and sell equal # of options –> limited upside and downside
Money Spreads = options have diff strikes (but same underlying and expiry)
Debit spread = you pay more than you get in premiums
Credit Spread you receive more than you pay in premiums
Bull Spread = buy a low strike option and sell a higher strike option; profit if the underlying rises
pay more for low strike than you get for selling high strike for bull call (debit spread); for a bull put you receive more (credit spread) for selling the lower strike than you do to buy the higher strike, so you get a net INFLOW of premium
max loss = net premium
limited upside
both Bull call AND Put spread = buy low strike and sell high –> bull put means you’re long the put

Bear Spreads
General spread info:
Spreads = buy and sell equal # of options –> limited upside and downside
Money Spreads = options have diff strikes (but same underlying and expiry)
Debit spread = you pay more than you get in premiums
Credit Spread you receive more than you pay in premiums
Bear Spreads = Sell LOWER strike, buy Higher strike –> they’re just short bull spreads –> profiles are just reflections in the x-axis (flip over like turning back a page)
NOTE: If a question is ambiguous, use CALLs for BULL spread and PUTS for a BEAR spread

The Greeks: Delta and Gamma

The Greeks: Theta and Vega

Position Deltas

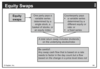
Delta of a Covered Call
Covered call = long underlying, sell call

Call Values Pre-Expiration

Put Values Pre-expiration

Delta of a Protective Put

Hedging a Short Position

Calendar Spreads
FOCUS ON WHERE YOU BENEFIT (in terms of underlying and volatility moves)
Long = buy a longer-dated option and sell a shorter-dated option at the same strike and underlying
Short = sell longer dated and buy shorter dated
both options the same (either two calls or two puts)
How to tell if you should be long or short: at expiry of the nearer-dated option, both will have the same intrinsic value, which cancels out (bc we’re both long and short) BUT the LONG position will also still have time value –> as long as time value > initial net premium paid, you gain
SO:
go LONG if close to or at ATM and expecting low price movement between now and the shorter-term expiry
go SHORT if expecting a big move in the underlying or a decrease in implied volatility
–> if your LT view on value of stock is bullish, want long call spread

Volatility Skew and Smile
two common observed patterns
Smile = further-from-ATM options have higher implied volatilities –> imagine plotting implied volatility vs. strike –> you’d see a u-shaped curve (smile)
Skew = implied volatility increases for more OTM puts, and decreases for more OTM calls –> more common than smile
–> because in a bear scenario, more demand from hedgers for OTM puts to protect their downside, bidding up value and therefore implied volatility
–> if you see a sharp increase in the level of skew plus a surge in implied volatility, means mkt is turning bearish –> little demand for OTM calls (hence why DECREASE in OTM call vol)
HOW TO PROFIT FROM IT IN PHOTO:

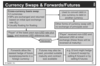
Interest Rate Swap Notional Principal Formula
MEMORIZE FORMULA AND BOTTOM BOX OF SLIDE (positive D etc)
used to amend portfolio duration
Ns = notional swap principal
MDt = target MD
MDp = current portfolio MD
MDs = MD of the swap
MVp = MV of portfolio
SWAP DURATION = net of the MDs of equivalent positions in fixed-and-floating rate bonds
–> D or what you receive minus D of what you pay –> eg MDpayfixed = MDfloat = MDfixed –> negative bc fixed bond duration > that of FRN

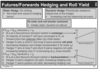
How to Hedge against ST Interest Rate Changes
for futures: if fear rates will rise, then quote will fall, so hedge by selling futures (sell high, buy cheap, if rates do rise)
–> # of contracts for hedge = principal for actual loan / reference deposit

Fixed Income Futures
FI:
changes in the price of a FI future are driven by changes in the TD bond price –> work in terms of BPv
NOTE: DONT FORGET to MULTIPLY BY CONVERSION FACTOR