CT3 - Probability & Statistics

Question 1

How do you derive a moment from a moment generating function (m.g.f)?

Answer 1

Continuous function MGF:
integral of e^txf(x)

Discrete function MGF: sum[0,∞] of e^txf(x)

Differentiate MGF i times for i’th moment and then evaluate derivative of M(t) at t=0

e.g. for second moment - E(X²), use M’‘(t) at t = 0

Question 2

What is a Standard Error?

Answer 2

The standard error (SE) is given by

Question 3

DBN of Sample Variance v. Population Variance

Answer 3

For a sample of size n with a sample variance S² from a population with a population variance of σ² where (n - 1) is degrees of freedom:

Question 4

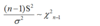
What is a Z-Score?

Answer 4

For a given point estimate (e.g. mean of a sample), the Z-score (z) is given by the following (σ should be the population SD, but may be substituted with the sample SD if the value for the population is not known and the sample is not too small)

Question 5

What is the Expectation and Variance of a Chi-Square Distribution?

Answer 5

If X has the chi-square distribution with n degrees of freedom then

E(X)=n
var(X)=2n

Question 6

What are the First and Second Moments of the Binomial Distribution?

Answer 6

Question 7

What is the Central Limit Theorem?

Answer 7

Question 8

Define the Significance Level α

Answer 8

Significance Level α given by:

α = P(reject H₀ when H₀ is true)

Question 9

Define Sample Variance

Answer 9

Sample variance S², for a sample of size n, is given by:

Question 10

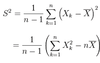
Prove that Sample Variance should be Equal to Population Variance

Answer 10

Question 11

What is an F distribution?

Answer 11

Question 12

What is the Cramer-Rao Lower Bound (CRLB)?

Answer 12

The Frechet-Cramer-Rao (or just Cramer-Rao) Lower Bound (CRLB) provides the lower bound for the variance of an unbiased estimator. If an estimator’s variance is equal to the CRLB, then it is described as optimal - i.e. no estimator can be more efficient.

Question 13

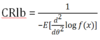
What is the Covariance Formula for Calculating the Correlation Coefficient?

Answer 13

Question 14

What is the Raw Score Formula for Calculating the Correlation Coefficient?

Answer 14

Question 15

What is the t-statistic for testing the sample correlation coefficient?

Answer 15

For a sample, it is the sample correlation coefficient r, rather than the population correlation coefficient ρ that is calculated. As such, r is an estimate of ρ.

If ρ=0, r ≈ 0

The distribution of r, given ρ = 0 is given by the test statistic t, which has a Student t distribution with n - 2 degrees of freedom.

Question 16

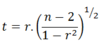
What is the Least Squares Line of Regression?

Answer 16

If two variables X and Y appear to have a correlation, then the approximate dependence between X and Y may be modelled using a polynomial.

For a linear dependence of the form y = ax + b the principle of least squares may be used i.e., L = E[Y - aX - b]² aand derivatives taken w.r.t a and b and equated to zero in order to derive:

Question 17

How are the Moments about the Mean Derived from the Cumulant Generating Function for n=2, n=3

Answer 17

Question 18

Compound Distribution Mean and Variance
for N=n

Answer 18

Question 19

Compound Distribution - Compound Mean

Answer 19

Question 20

Compound Distribution - Compound Variance

Answer 20

Question 21

Variance of Sum of Uncorrelated Variables and their Mean

Answer 21

Question 22

What is the Method of Moments?

Answer 22

The method of moments is a method of estimation of population parameters such as mean, variance, median, etc. (which need not be moments), by equating sample moments with unobservable population moments and then solving those equations for the quantities to be estimated.

Question 23

What is the Central Tendency of a Distribution?

Answer 23

The central tendency of a distribution locates the “center” of a distribution of values.

The three major types of estimates of central tendency are

• the mean
• the median
• and the mode.

Question 24

How do you Calculate the First and Third Quartiles of a Data Set

Answer 24

To calculate the lower and upper quartiles, split the data set in two (if there is an odd number of data items, exclude the median from the calculation).

First Quartile is median of first half of split data set

Second Quartile is median of second half of split data set

Question 25

What is Skewness?

Answer 25

Skewness is a measure of the asymmetry of the probability distribution. The skewness value is a real number, i.e. can be positive or negative. In some situations skewness can be undefined.

Qualitatively, a negative skew indicates that the tail on the left side of the distribution is longer than the right side.

Question 26

What is a Probability Tree?

Answer 26

Question 27

What is a Sample Space, an Event (Elementary / Compound)

Answer 27

The sample space is an exhaustive list of all the possible outcomes of an experiment.

Each possible result of such a study is represented by one and only one point in the sample space, which is usually denoted by Ω.

An event is any collection of outcomes of an experiment.

Formally, any subset of the sample space is an event.

Any event which consists of a single outcome in the sample space is called an elementary or simple event.

Events which consist of more than one outcome are called compound events.

Question 28

How to Calculate r Permutations from n

_nP_r

Answer 28

Question 29

Key Properties of

n Choose r

Answer 29

Question 30

Normal Approximation to the Binomial

Answer 30

If np and n(1 - p) > 5

Can approximate binomial using normal distribution with a continuity adjustment

In Binomial,

P(X ≤ x) = P(X < x + 1)

For Y, Normally Distributed random variable approximating binomial X:

P(X < x + 1) ≈ P (Y ≤ x + 1/2)

Where X is a binomially distributed random variable and Y is a normally distributed random variable with the same expectation and variance as X

• E[Y]=E[X]=np*
• Var(Y) = Var(X) = np(1-p)*

Question 31

What is the Quadtratic Solution
for ax² + bx + c = 0

Answer 31

Question 32

Define Likelihood Function and Maximum Likelihood Estimate (MLE)

Answer 32

NB: When taking initial Log L(θ), any constant terms can be lumpted together as “constant”, as they will be lost in the first differentation.

Question 33

What is Integration by Parts

Answer 33

Integration by parts is a theorem that relates the integral of a product of functions to the integral of their derivative and antiderivative.

Question 34

ρ, r, R² - coefficients

Answer 34

• ρ* - population correlation coefficient
• r* - sample correlation coefficient (estimator for ρ)
• R²* - coefficient of determination = r²
• (where intercept is included, for linear regration)*

Question 35

Assumptions of ANOVA

Answer 35

In an ANOVA model, the j^th value in the i^th treatment (group) - Y_ij, is assumed to take the value:

Y_ij = μ + τ_i + e_ij

μ - population (grand) mean

τ_i - ith treatment effect

e_ij - normally distributed residual error

• Independence of observations (iid) – this is an assumption of the model that simplifies the statistical analysis.
• Normality
  the distributions of the residuals are normal.
• Common variance of data in the groups - “homoscedasticity”
  the variance of data in groups should be the same.

Question 36

Define Mean Squared

(MSE)

Answer 36

Mean Squared Error (MSE) is a measure of the goodness of fit of an estimator, defined as:

Question 37

nth Central Moment

Answer 37

Question 38

Fisher Transformation for Sample Correlation Coefficient

Answer 38

If r is the sample correlation coefficient for (X,Y) with a bivariate normal distribution, then the value z given by the Fisher z transformation is approximately normally distributed:

Question 39

What is the Bernoulli Distribution?

Answer 39

The Bernoulli Distribution is simply the BInomial Distribution with n=1

i.e. It is a discrete distribution for one even where the probability of it happening = p and the probability of it not happening q = 1 - p

Question 40

Point Estimation of Error Variance for Linear Regression

Answer 40

Question 41

MGF of a Sum of Random Variables

Answer 41

Let X and Y be independent random variables.

Let Z = X + Y. Then the mgf of Z is given by

M_Z(t) = M_X(t)M_Y(t)

If X1, X2, · · · , Xn are independent and identically distributed, then

M_{X1+X2+···+Xn}(t) = [M(t)]ⁿ

where *M(t) = M_Xj(t) *
is the common mgf of the X_j’s.

Proof.

E[e^tZ] = E[e^t(X+Y)] = E[e^tXe^tY]

= E[e^tX] E[e^{<span>tY</span>}] = M_X(t)M_Y(t)

Question 42

What is the Dbn of a linear Combination of Χ² (chi-square) variables

Answer 42

If there are n chi-square variables, each with r_i degrees of freedom

X₁ ~ Χ² (r₁)
X₂ ~ Χ² (r₂)
….
X_n ~ Χ² (r_n)

• Y = X₁ + X₂ + … + X_n*
• Y ~ Χ²(r₁ + r₂ + … + r_n)*

Question 43

What is the Dbn of a Linear Combination of Normal Variables?

Answer 43

If there is a linear combination of N normal variables:

X₁ ~ (μ₁,σ₁²)
X₂ ~ (μ₂,σ₂²)
…
X₂ ~ (μ₂,σ₂²)

• Y = X₁+X₂+…+X_n*
• Y~ (μ₁+μ₂+… +μ_n, σ₁²+σ₂²+…+σ_n²)*

Question 44

DBN of RSS and Error Variance

Answer 44

If RSS is residual sum of squares for n data points in relation to a particular line of regression, the estimator for the variance of the error is given by:

Question 45

Prove E[E[Y|X]] = E[Y]

Answer 45

Question 46

What Happens to Correlation Coefficient Under Linear Transformation of Data?

Answer 46

If a paired data set has a sample correlation r, if the data is transformed using a series of one or more linear transformations:

Sign may change, depending on transformation

r_old| = | r_transformed|