Circles

Question 1

circle

Answer 1

a set of points at a given distance (radius) from a given point (center) in a given place

Question 2

radius

Answer 2

(the length of the) segment joining the center and a point on the circle

Question 3

chord

Answer 3

the segment joining two points on the circle

Question 4

diameter

Answer 4

(the length of the) chord passing through the center

Question 5

secant

Answer 5

line passing through the two points of the circle

Question 6

tangent

Answer 6

(to a circle) a line passing through one point of the circle (which is called the point of tangency)

Question 7

central angle

Answer 7

an angle whose vertex is the center (its sides are radii)

angle = arc

Question 8

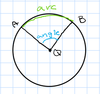
measure of an arc

Answer 8

the measure of the central angle is subtends (cut off)

Question 9

minor arc

Answer 9

arc with measure < 180°

Question 10

semicircle

Answer 10

arc with measure = 180°

Question 11

major arc

Answer 11

arc with measure > 180°

Question 12

inscribed angle

Answer 12

angle with vertex on circle

measures half the measure of the arc it intercepts

angle = 1/2 arc

Question 13

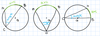
chord-tangent angle

Answer 13

angle formed by a chord and a tangent line

angle = 1/2 arc

Question 14

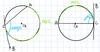
chord-chord angle

Answer 14

angle formed by two intersecting chords

angle = 1/2(arc₁ + arc₂)

Question 15

secant-secant angle

Answer 15

angle formed by two secants

angle = 1/2(arc₁ - arc₂)

Question 16

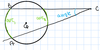
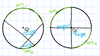
secant-tangent angle

Answer 16

angle formed by a secant and a tangent

angle = 1/2(arc₁ - arc₂)

Question 17

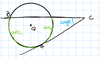
tangent-tangent angle

Answer 17

angle formed by two tangents

angle = 1/2(arc₁ - arc₂)

Question 18

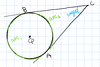
chord-chord power theorem

Answer 18

when two chords intersect, the product of one part of the chord and the other is equal to the same product in the other chord

Question 19

concentric

Answer 19

two or more coplanar circles with the same center

Question 20

inscribed

Answer 20

all the vertices of the polygon lie on the circle

Question 21

circumscribed

Answer 21

all the sides of the polygon are tangent to the circle

Question 22

tangent-secant power thm

Answer 22

if a tangent and secant intersect, then the square of the measure of the tangent segment is equal to the product of the measures of the the entire secant segment and its external part

Question 23

secant-secant power thm

Answer 23

if two secants intersect, then the product of the measure of one secant segment and its external part is equal to the product of the measures of the other secant segment and its external part