Alt-On-Hyp, Trip and Similarity

Question 1

Geometric Mean

Answer 1

x of a and b such that

x² = ab

Question 2

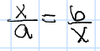
Alt-On-Hyp

Answer 2

The altitude to the hypotenuse of a right triangle is the geometric mean of the segments that the hypotenuse is divided into by the alititude

Question 3

Leg-Alt-On-Hyp

Answer 3

If we draw an altitude to the hypotenuse of a right triangle, then each leg is the geometric mean of the hypotenuse and the adjacent segment of the hypotenuse

Question 4

sin(x)

Answer 4

opposite leg

hypotenuse

Question 5

cos(x)

Answer 5

adjacent leg

hypotenuse

Question 6

tan(x)

Answer 6

opposite leg

adjacent leg

(slope of the hypotenuse)

Question 7

sin(30°)

Answer 7

1/2

Question 8

cos(30°)

Answer 8

sqrt(3)/2

Question 9

tan(30°)

Answer 9

sqrt(3)/3

Question 10

sin(60°)

Answer 10

sqrt(3)/2

Question 11

cos(60°)

Answer 11

1/2

Question 12

tan(60°)

Answer 12

sqrt(3)

Question 13

sin(45°)

Answer 13

sqrt(2)/2

Question 14

cos(45°)

Answer 14

sqrt(2)/2

Question 15

tan(45°)

Answer 15

1

Question 16

Law of Sines

Answer 16

sin(A) sin(B) sin(C)

———- = ——– = ——–

a b c

Question 17

Law of Cosines

Answer 17

a² = b² + c² - 2bccosA

b² = a² + c² - 2accosB

c² = a² + b² - 2abcosC

Question 18

Identities with Supplementaries

Answer 18

sinA = sin(180-A)

-cosA = cos(180-A)

Question 19

Inverse Trig Functions

Answer 19

sin^-1(opp/hyp) = x

cos^-1(adj/hyp) = x

tan^-1(opp/adj) =x

Question 20

To solve SSS and SAS

Answer 20

Use Law of Cosines

Question 21

To solve ASA, ASS and AAS

Answer 21

Use Law of Sines

Question 22

To solve HL

Answer 22

Use Pythag and Trig

Question 23

a < bsinA

Answer 23

No possible triangles

Question 24

a = bsinA

Answer 24

One possible triangle

Question 25

bsinA < a < b

Answer 25

two possible triangles

Question 26

a >/= b

Answer 26

one possible triangle